一、坐标系与位姿变换
一、坐标系与位姿变换
1.坐标系
为了描述机器人本身的位置和姿态,必须构建坐标系来描述机器人的状态(世界坐标系、机体坐标系)。
在平面内一般包含2个移动自由度(x轴、y轴)及1个转动自由度(平面内绕某点)。
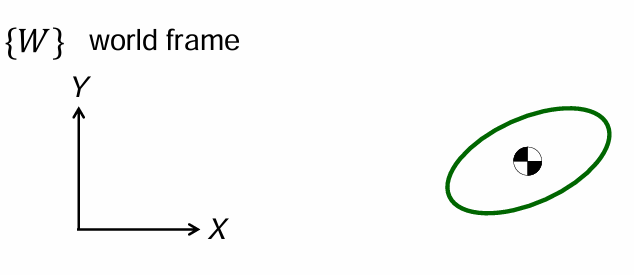
在空间中一般包含3个移动自由度(x轴、y轴、z轴)及3个转动自由度(绕x轴、y轴、z轴)。
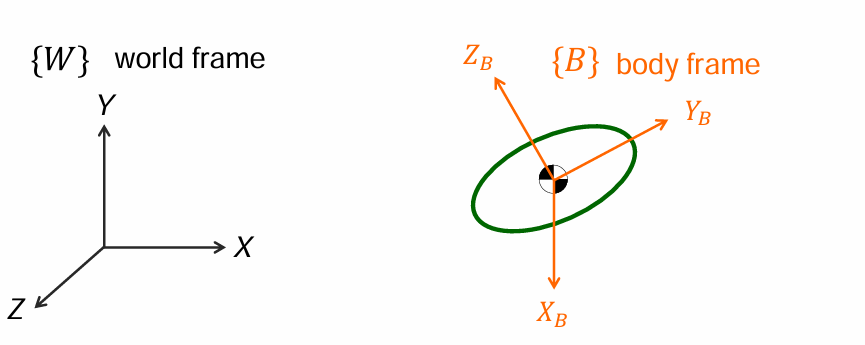
2.移动
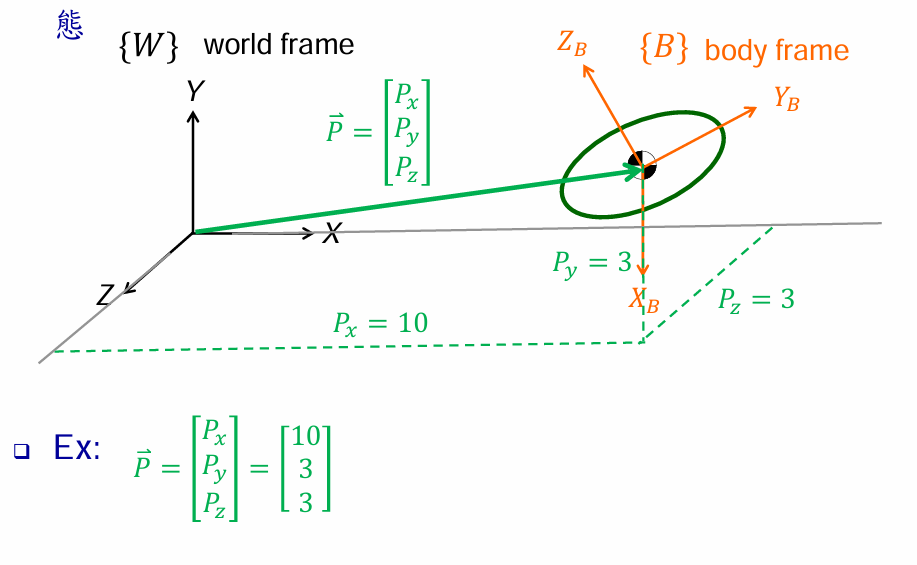
平移描述的是物体在空间中位置的变化,即物体在某个方向上移动而不改变其形状和姿态。这种移动可以理解为物体的每个点都沿着相同的方向和距离移动。通过向量描述刚体在空间中的位置(分别在3个轴投影的分量来具体描述)。
3.旋转
3.1旋转矩阵
旋转是刚体绕平面内一点或某个轴的转动,其位置和方向会发生变化,但形状和大小保持不变。旋转描述了物体相对于某个参考点的朝向变化,通常用于表示物体的姿态调整。
我们知道点的位置可以用矢量描述,而物体的姿态我们可以用固定在物体上的坐标系来描述。
我们想要知道物体{B}相对于坐标系{A}的姿态时,可以将坐标系{B}的三个主轴方向的单位矢量分别相对于坐标系{A}的各轴的分量按照X、Y、Z的顺序组成一个3×3的矩阵,我们称这个矩阵为——旋转矩阵。
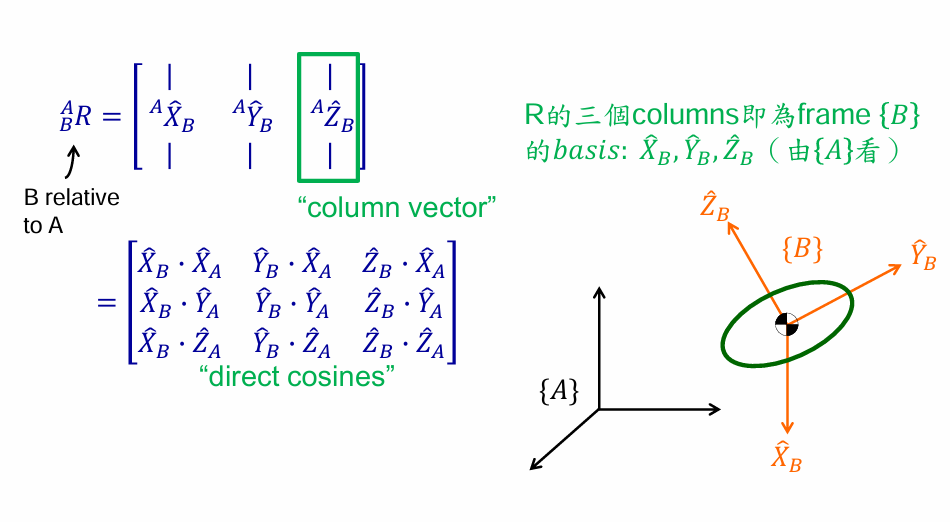
旋转矩阵的特性


旋转矩阵的常见形式
1、绕x轴旋转角度θ
绕x轴旋转时,x坐标不变,y和z坐标发生变换:
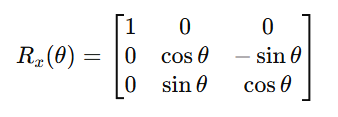
2.绕y轴旋转角度θ
绕y轴旋转时,y坐标不变,x和z坐标发生变换:
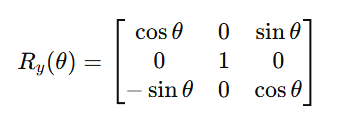
3.绕z轴旋转角度θ
绕z轴旋转时,z坐标不变,x和y坐标发生变换:
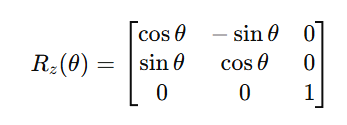
旋转矩阵的三种用法
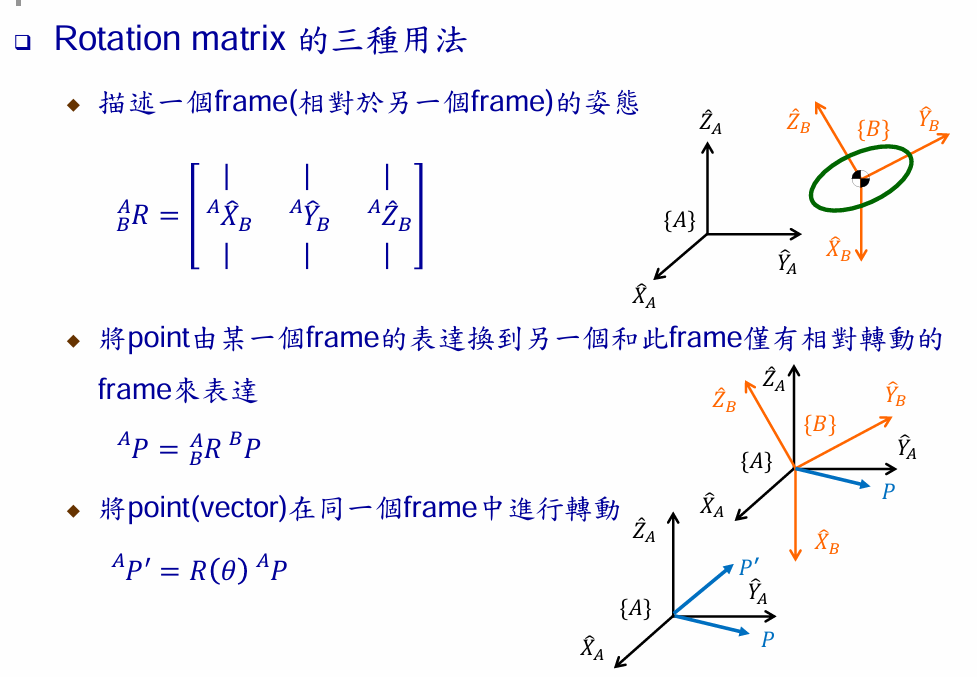
齐次变换矩阵
在三维空间中,刚体的位姿(Pose)= 位置(Position, 平移)+ 姿态(Orientation, 旋转)。我们在旋转矩阵的基础上加入位移,通常使用一个4×4的齐次矩阵来表示:


3.2欧拉角
- 欧拉角用 三个角度 来描述空间中的一个旋转。
- 本质:把一个坐标系通过 依次绕某些轴的旋转 变换到另一个姿态。
常见的旋转顺序:
- Z-Y-X(yaw-pitch-roll) 航空航天、机器人学常见
- Z-Y-Z 机械臂运动学(DH 参数法)常见
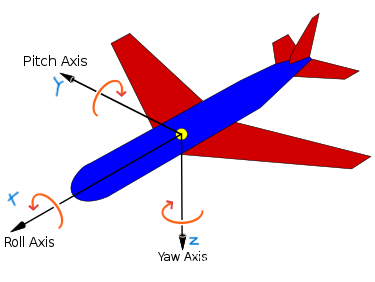
以常见的 Z-Y-X (Yaw-Pitch-Roll) 为例:
-
滚转角 (roll,绕 X 轴旋转)
-
俯仰角 (pitch,绕 Y 轴旋转)
-
偏航角 (yaw,绕 Z 轴旋转)
欧拉角的优缺点
✅ 优点:
- 直观(和飞机的航向、俯仰、翻滚一致)
- 只用 3 个参数(比旋转矩阵 9 个参数更简洁)
⚠️ 缺点:
-
存在 万向节锁死 (gimbal lock),某些角度下失去一个自由度
-
不唯一:不同的旋转顺序、不同角度组合可能表示同一个姿态
注:万向节 (Gimbal) 是一种用三个转环实现三维旋转的机构,每个环负责一个角度(yaw, pitch, roll)。当中间的环转到某个角度时(通常是 ±90°),两个旋转轴会重合。这样原本独立的 3 个自由度瞬间变成 2 个自由度,系统丢失了一个旋转方向。这就是所谓的 万向节锁死。
总结
- 欧拉角:用 3 个角度 表示旋转
- 通过三个基本旋转矩阵相乘得到整体旋转
- 常用形式:Z-Y-X (yaw-pitch-roll)
- 优点:直观简洁
- 缺点:存在奇异性,数值计算上常用 旋转矩阵 或 四元数
3.3四元数
1. 定义
一个四元数可以写作:
其中:
- w:实部
- x, y, z:虚部(向量部分)
在旋转应用中,四元数通常记为:
2. 单位四元数与旋转
旋转用 单位四元数(模长 = 1)表示:
等价于:
其中:
-
旋转角:
-
:旋转轴单位向量
注 旋转轴的几何意义:
- 旋转轴就是一个 固定的方向向量,代表物体绕着它进行旋转。
- 单位化(长度为 1)保证四元数的模长为 1,从而表示纯旋转(不缩放)。
- 比如:
- 绕 X 轴 旋转
- 绕 Y 轴 旋转
- 绕 Z 轴 旋转
- 绕 X-Z 平面 45°方向的轴 旋转
3. 四元数与旋转矩阵互换
从四元数到旋转矩阵:
设 ,则:
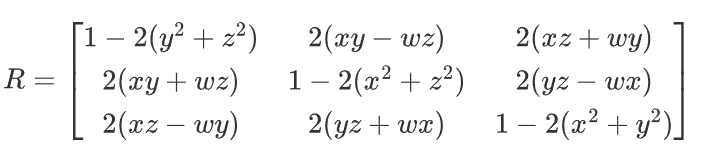
从旋转矩阵到四元数:
如果 已知,可以用:
4.四元数的优缺点
✅ 优点:
- 没有奇异性(不像欧拉角的万向节锁死)
- 表达简洁(4 个参数,比旋转矩阵 9 个参数少)
- 易于插值(适合动画、路径规划:球面线性插值 Slerp)
⚠️ 缺点:
- 不如欧拉角直观
- 需要保持归一化(数值计算时会有误差积累)
5. 总结
-
四元数用 4 个数表示旋转,克服了欧拉角的缺陷
-
在机器人学、计算机图形学、无人机控制中广泛使用
-
常和旋转矩阵、欧拉角互相转换
4.三维旋转的多种表示方法比较
| 方法 | 参数数量 | 表达直观性 | 是否唯一 | 是否有奇异性 | 运算复杂度 | 常见应用 |
|---|---|---|---|---|---|---|
| 旋转矩阵 (Rotation Matrix) | 9 个参数(3×3矩阵,约束后有效参数 3 个) | 中等(通过矩阵作用可以直观理解) | 唯一 | 无 | 矩阵乘法,开销较大 | 机器人运动学、坐标变换 |
| 欧拉角 (Euler Angles) | 3 个参数 | 非常直观(航向、俯仰、翻滚) | 不唯一(不同旋转顺序表示相同姿态) | 有(万向节锁死) | 简单 | 飞行器姿态、机械臂 DH 参数 |
| 四元数 (Quaternion) | 4 个参数(1 个约束,实质 3 个) | 不直观 | 唯一(单位四元数) | 无 | 乘法运算高效,易于插值 | 机器人控制、无人机、图形学、SLAM |
总结
-
旋转矩阵:适合直接做坐标变换,稳定但冗余(9 参数)。
-
欧拉角:最直观,但有奇异性,不适合连续旋转计算。
-
四元数:数值稳定、计算高效、插值自然 机器人、图形学首选。
Q&A
1.为什么需要用一个整体的“齐次矩阵”来表示位姿,而不是分开用旋转和位移?
分开⽤旋转和位移,在进⾏连续变换时需要分别处理旋转和平移,且在进⾏连续变换时需要分别处理 旋转和平移,⽤⼀个整体的“⻬次矩阵”来表⽰位姿,有如下好处:
- 统⼀表⽰:将旋转和平移整合在单个4×4矩阵中
- 链式变换简化:通过矩阵乘法即可实现连续的坐标系变换
- 数学⼀致性:所有变换都可⽤相同的矩阵乘法规则处理
- 计算效率:便于计算机实现和优化
2.如果⼀个点在A坐标系下有坐标,我们如何把它转换到B坐标系?
给定点P在A坐标系下的坐标PA,要转换到B坐标系下的坐标PB,转换公式为:
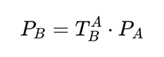
1)确定A坐标系相对于B坐标系的位姿
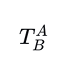
2)将点P在A下的坐标表⽰为⻬次坐标:
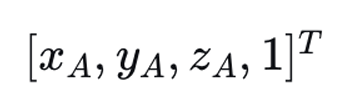
3)进⾏矩阵乘法运算
4)得到点在B下的⻬次坐标,提取前三个分量即为直⻆坐标
3.多个关节坐标系之间的变换,最后是如何得到末端相对基座的位姿的?
末端相对基座的位姿 = 从基座开始,逐级乘上所有中间关节的齐次矩阵

这样 就是末端执行器在基座坐标系下的完整位姿(包含旋转 + 平移)。