三、机器人运动学

一、运动学与动力学概念

运动学（Kinematics）
研究“运动本身”，不考虑产生运动的力。
主要关注：

• 位置 $\mathbf{x}$
• 速度 $\mathbf{v} = \dfrac{d\mathbf{x}}{dt}$
• 加速度 $\mathbf{a} = \dfrac{d\mathbf{v}}{dt} = \dfrac{d^2\mathbf{x}}{dt^2}$

机器人运动学（Robot Kinematics）研究机器人关节、连杆之间的几何关系。

• 正运动学（Forward Kinematics, FK）：已知关节变量，求末端执行器位姿。
• 逆运动学（Inverse Kinematics, IK）：已知末端执行器位姿，求关节变量。

动力学（Dynamics）
研究“力如何产生运动”，依据牛顿第二定律：

$$\mathbf{F} = m\mathbf{a}$$

---

二、机械手臂的几何结构描述

1. 组成要素

• Link（连杆）：刚体，用来连接各关节。
• Joint（关节）：提供一个自由度（DOF）。
  • 旋转关节（Revolute） → 变量为角度 $\theta$
  • 移动关节（Prismatic） → 变量为位移 $d$

• 末端执行器（End Effector）：机器人用于执行任务的末端装置（如机械手爪）。

• 姿态（Pose）：包含位置与方向：

$$\mathbf{p} = [x, y, z]^T, \qquad \mathbf{R} \in SO(3)$$

2. 编号规则

• Link 0：基座（固定不动）
• Link 1：第一个活动杆
• 以此类推，最后一个为末端执行器。

---

二、正运动学（Forward Kinematics, FK）

2.1 定义

给定各关节变量，求出末端相对于基座的位姿：

$$\mathbf{T}_{0}^{n} = f(\theta_1, \theta_2, \dots, \theta_n)$$

其中 $\mathbf{T}_{0}^{n}$ 是齐次变换矩阵：

$$\mathbf{T} = \begin{bmatrix} \mathbf{R} & \mathbf{p} \\ 0 & 1 \end{bmatrix}$$

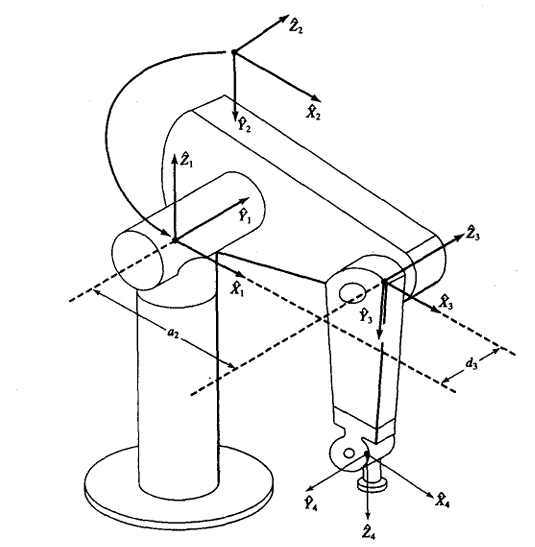
2.2 D–H 参数法（Denavit–Hartenberg）

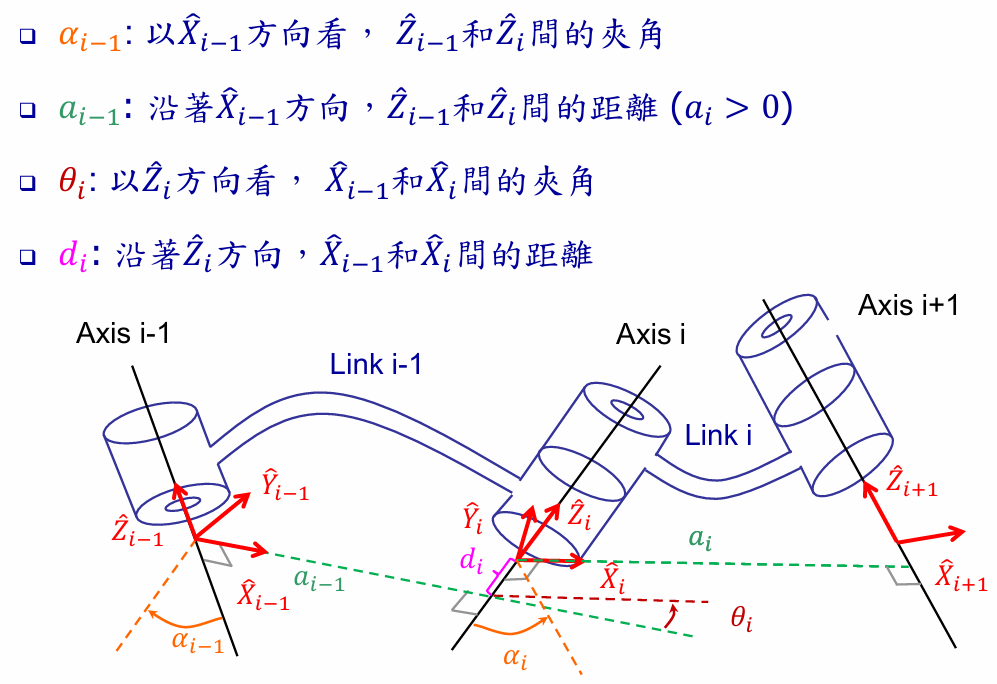
为每个连杆定义 4 个参数：

参数	含义	类型
$a_i$	连杆长度	位移
$\alpha_i$	连杆扭角	旋转
$d_i$	连杆偏距	位移
$\theta_i$	连杆转角	旋转

单个连杆的齐次变换（从 $i-1$ 到 $i$）：

$$\mathbf{A}_i = \begin{bmatrix} \cos\theta_i & -\sin\theta_i\cos\alpha_i & \sin\theta_i\sin\alpha_i & a_i\cos\theta_i \\ \sin\theta_i & \cos\theta_i\cos\alpha_i & -\cos\theta_i\sin\alpha_i & a_i\sin\theta_i \\ 0 & \sin\alpha_i & \cos\alpha_i & d_i \\ 0 & 0 & 0 & 1 \end{bmatrix}$$

整体变换为：

$$\mathbf{T}_{0}^{n} = \mathbf{A}_1 \mathbf{A}_2 \cdots \mathbf{A}_n$$

2.3 二维双连杆机械臂示例

已知两关节转角 $\theta_1, \theta_2$，连杆长度 $l_1, l_2$，则末端坐标为：

$$\begin{cases} x = l_1\cos\theta_1 + l_2\cos(\theta_1 + \theta_2) \\ y = l_1\sin\theta_1 + l_2\sin(\theta_1 + \theta_2) \end{cases}$$

示意图（Mermaid）：

flowchart LR
  Base[Base]
  Base -->|θ1| Link1[Link1]
  Link1 -->|θ2| Link2[Link2]
  Link2 --> End[End Effector]

---

三、逆运动学（Inverse Kinematics, IK）

3.1 定义

已知末端位姿 $\mathbf{T}_{0}^{n}$，求各个关节变量：

$$\text{Given } \mathbf{T}_{0}^{n}, \quad \text{find } \theta_i$$

3.2 特点

• 非唯一性：可能有多个解（如肘上/肘下姿态）。
• 可能无解：目标点在工作空间之外。
• 高非线性：方程复杂，常需数值迭代法。

3.3 几何法求解（二维双连杆示例）

先求 $\theta_2$：

$$\cos\theta_2 = \frac{x^2 + y^2 - l_1^2 - l_2^2}{2 l_1 l_2}$$

$$\theta_2 = \arccos(\cos\theta_2)$$

再求 $\theta_1$：

$$\theta_1 = \operatorname{atan2}(y, x) - \operatorname{atan2}\bigl(l_2\sin\theta_2,; l_1 + l_2\cos\theta_2\bigr)$$

条件：$|\cos\theta_2| \le 1$，即目标点在可达范围内。

3.4 数值法（Jacobian 迭代法）

雅可比关系：

$$\dot{\mathbf{x}} = \mathbf{J}(\theta)\dot{\theta}$$

伪逆求解增量：

$$\dot{\theta} = \mathbf{J}^{+}(\theta)\dot{\mathbf{x}}$$

迭代更新：

$$\theta_{k+1} = \theta_k + \Delta t\mathbf{J}^{+}(\theta_k)\bigl(\mathbf{x}_{\text{target}} - \mathbf{x}(\theta_k)\bigr)$$

---

四、FK 与 IK 对比总结

项目	正运动学 (FK)	逆运动学 (IK)
输入	关节变量 $\theta_i$	末端位姿 $\mathbf{T}_{0}^{n}$
输出	末端位姿 $\mathbf{T}_{0}^{n}$	关节变量 $\theta_i$
计算难度	简单（矩阵乘积）	复杂（非线性方程）
解的数量	唯一	多解 / 无解
应用场景	仿真、验证	规划、控制

五、Q&A

1.正运动学和逆运动学的输入和输出是什么？

正运动学：

1）输入
各个关节变量（旋转角或平移量）：

$$\theta_1, \theta_2, \dots, \theta_n$$

2）输出

末端执行器的位姿（位置 + 姿态）：

$$\mathbf{T}_0^n = \begin{bmatrix} \mathbf{R} & \mathbf{p} \\\\ 0 & 1 \end{bmatrix}$$

其中：

• 位置：末端的坐标 $(x, y, z)$

• 姿态：末端的方向（用旋转矩阵、欧拉角或四元数表示）

逆运动学：

1）输入

目标末端位姿（期望的目标位置与方向）：

$$\mathbf{T}_{\text{target}} = \begin{bmatrix} \mathbf{R}_{\text{target}} & \mathbf{p}_{\text{target}} \\\\ 0 & 1 \end{bmatrix}$$

2）输出

关节变量：

$$\theta_1, \theta_2, \dots, \theta_n$$

---

2.一个平面两关节机械臂去到同一个目标点，可能会有几种解？为什么？

1）场景：

平面上一个两关节旋转机械臂（2R），每个连杆长度为 $l_1, l_2$，目标点为 $(x, y)$。

2）可能的解

通常有 两种几何解：

• 肘上（elbow-up）构型
• 肘下（elbow-down）构型

这两个解的区别在于第二个关节的弯曲方向不同

3）数学解释

由几何法可得第二关节角度：

$$\cos\theta_2 = \frac{x^2 + y^2 - l_1^2 - l_2^2}{2 l_1 l_2}$$

当 $|\cos\theta_2| \le 1$ 时，有两个可能的解：

$$\theta_2 = \arccos(\cos\theta_2)$$

和

$$\theta_2' = -\arccos(\cos\theta_2)$$

这对应两种不同的构型（即“肘上/肘下”）。

---

3.如果目标点超出了机械臂的最大工作范围，会怎样？

1）最大可达范围

末端与基座的最大、最小距离为：

$$r_{\max} = l_1 + l_2$$

$$r_{\min} = |l_1 - l_2|$$

2）超出范围时

如果目标点 $(x, y)$ 满足：

$$\sqrt{x^2 + y^2} > r_{\max}$$

或

$$\sqrt{x^2 + y^2} < r_{\min}$$

则机械臂 无实解（不可达），在计算中会出现：

$$|\cos\theta_2| > 1$$

导致 arccos() 无实数解。

3）物理意义

• 机械臂无法到达目标点。
• 控制系统通常会返回“不可达”或“超出工作空间”错误。
• 在规划算法中会直接排除这些点。

---

参考

1. 机器人学导论（原书第3版） ↩