自注意力机制与Transformer
自注意力机制与Transformer
1.自注意力机制
1.1自注意力机制的提出
由于传统的 RNN-based Encoder-Decoder 架构在建模过程中,下一个时刻的计算过程会依赖于上一个时刻的输出,而这种固有的属性就限制了传统的Encoder-Decoder 模型不能以并行的方式进行计算。
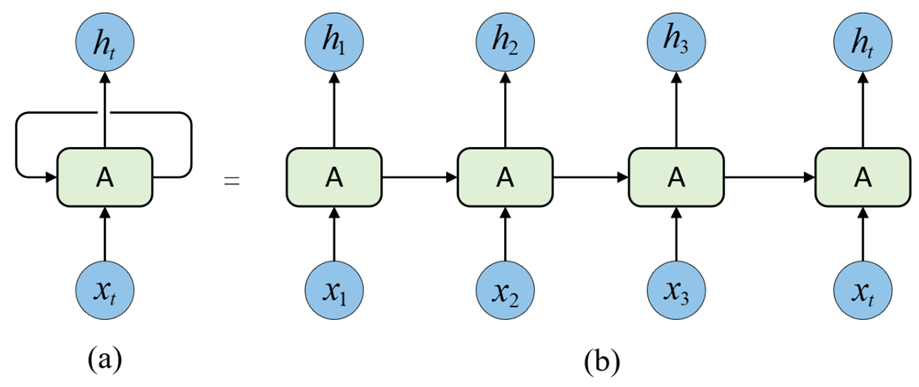
在Seq2Seq任务中,源输入序列的不同部分通常都具有不同的重要性,然而传统RNN-based Encoder-Decoder模型在处理这一过程时并没有考虑到这种情况,因为它只是依靠上一个时刻的解码输出来对当前时刻进行解码。如下图所示,当解码器对第三个时刻“是”进行解码时应该更加关注第2个时刻am对应的位置。传统的RNN-based Encoder-Decoder架构中无论输入句子多长,整个信息都被压缩成一个固定长度的向量(context vector)。当句子很长或信息复杂时,编码器很难在一个向量中保留所有关键信息,解码器生成后期内容时,早期信息容易被遗忘,导致长距离依赖丢失、翻译质量下降。
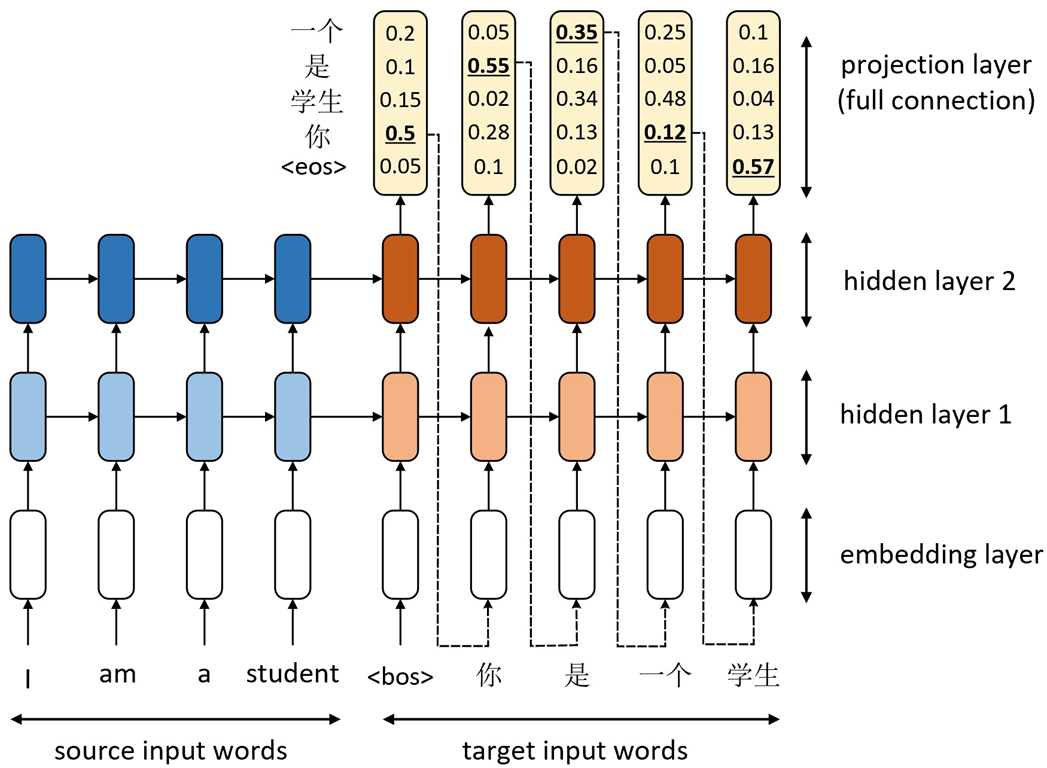
为了解决这一问题,Bahdanau 等人在 2014 年提出了注意力机制(Attention Mechanism),使得解码器在生成每个词时可以根据相关性动态关注输入序列的不同部分。注意力机制本质上通过计算输入特征之间的相似度分配权重,从而让模型“聚焦”于更相关的信息。
在此基础上,研究者进一步提出了自注意力机制(Self-Attention)。不同于传统的 Encoder-Decoder 注意力(跨序列),自注意力机制是在同一序列内部计算各元素之间的依赖关系。它摈弃了循环结构(RNN)和卷积结构(CNN),仅依靠多头自注意力机制(Multi-Head Self-Attention)来捕捉序列中任意两个位置之间的关系,从而实现并行计算并提升语义建模能力。
注意:自注意力机制与注意力机制是由有区别的
例如:我们需要给一个句子标注词性,同样的一个单词我们如何区分它在同一个句子中表达的不同含义?这就需要我们知道句子前后隐含的某种“关系”。因此,摈弃了传统的循环结构,取而代之的是只通过注意力机制来计算模型输入与输出的隐含向量表示(可以理解为不同向量之间的相关性), 这就是自注意力机制(Self-attention)
换句话说自注意力机制中模型在输出每个词时,可以“看看”输入序列的哪些部分更相关;计算一个加权平均,权重代表“注意力分配”;权重通过一个可学习的相似度函数(例如点积)得到。
✅ 自注意力机制的核心思想:
- 将整个序列作为输入,而非压缩成一个固定长度的向量;
- 输出每个词时,通过计算与输入序列中所有词的相关性(相似度)得到加权平均;
- 权重由可学习的函数(如点积相似度)计算得到。
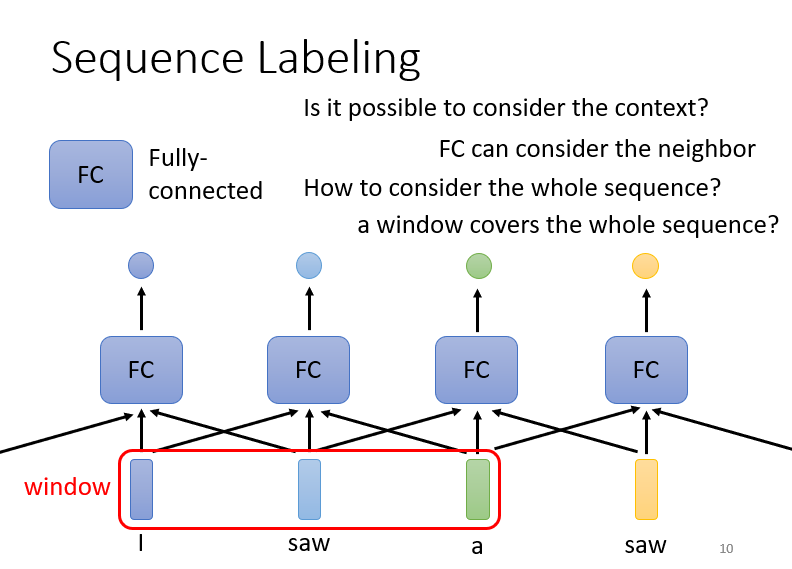
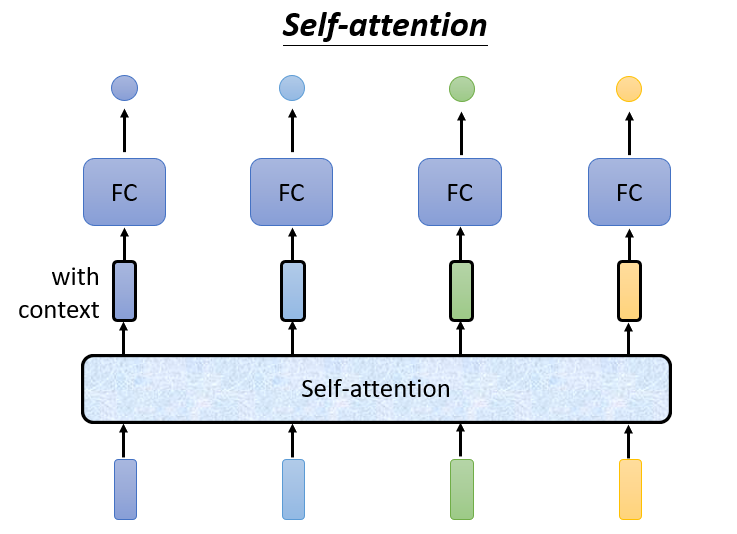
自注意力机制中可以将整个序列作为输入,而不只是某个固定长度的向量。
总的来说,自注意力机制的产生是为了解决传统序列模型在处理自然语言时的三大核心问题:
- 长距离依赖难以建模
- 计算效率低下以
- 语义理解能力有限
通过自注意力机制,Transformer模型能够并行处理整个序列,有效捕捉序列中任意两个位置之间的关系,从而在机器翻译、文本生成等任务中取得了突破性进展。
1.2自注意力机制计算
基于李宏毅《Self-Attention》课件整理
参考论文:Attention Is All You Need (Vaswani et al., 2017)
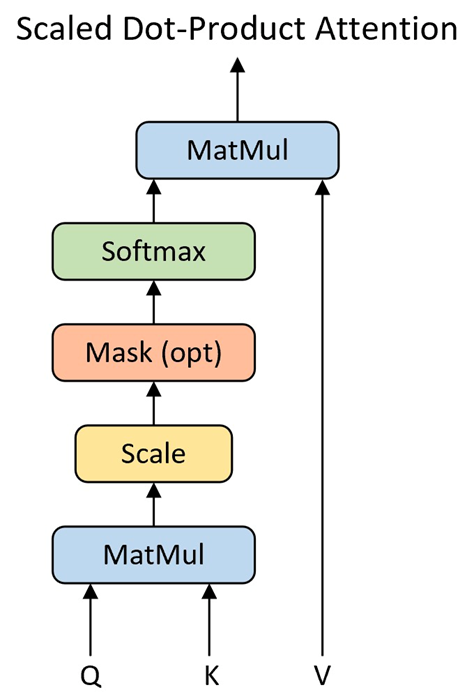
1.输入形式
self-attention的输入可能是你整个网络的输入也可能是某个隐藏层的输出
输入为一组向量:
这些向量可以表示:
- 句子中的词向量(NLP)
- 图像 patch 特征(Vision)
- 节点特征(Graph)
2.自注意力计算步骤
1️⃣ 线性映射(生成 Q, K, V)
每个输入向量通过三个线性层得到:
其中:
- Query (Q):代表“我想找什么信息”(查询者-当前关注的信息)
- Key (K):代表“我能提供什么信息”(被查询者,为其它查询者提供的说明-简介)
- Value (V):代表“具体的信息内容”(实际的内容-要输出的信息)
假设输入序列为“我 是 谁”,且已经通过某种方式得到了1个形状3×4的矩阵来进行表示,即图中的X。那么通过以下过程便能够就算得到Q、K 以及 V。
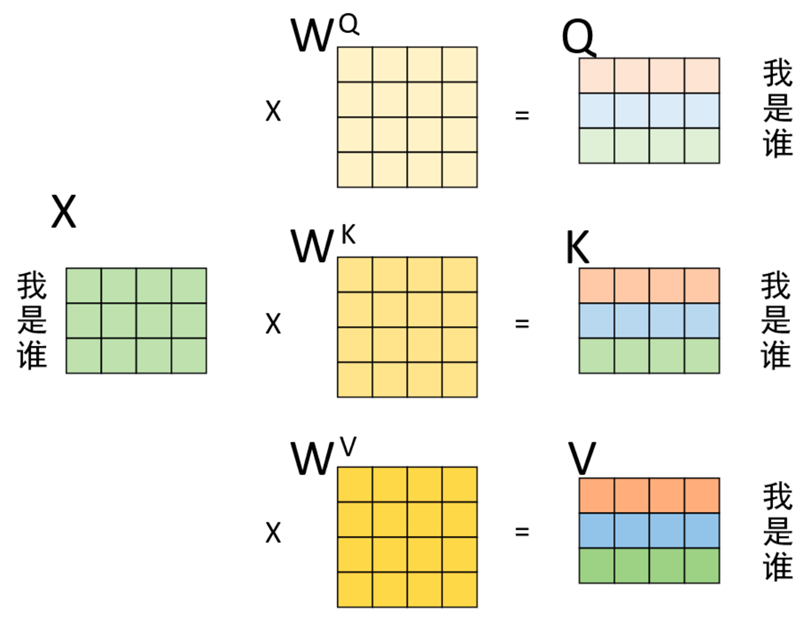
2️⃣ 计算注意力分数(相关性)
计算方式有很多种,点积(Dot-product)是最常见的一种。
使用点积(Dot-product)计算每个 Query 与所有 Key 的相似度:
矩阵形式:
在计算得到 Q、K、V后,就可以进一步计算得到权重向量, 计算过程如图所示。
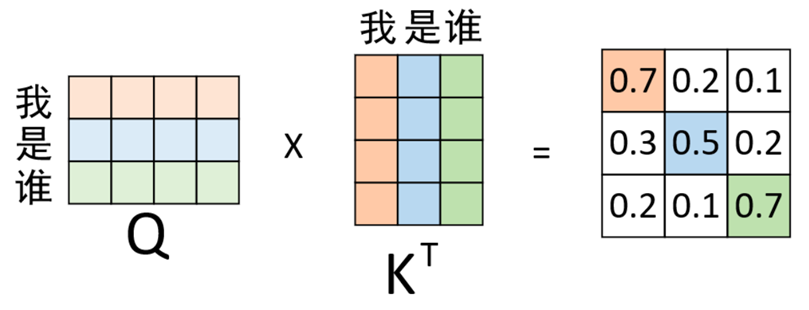
每一行表示当前元素对整个序列的关注程度。(这句话可能有些难以理解)具体来说:
该矩阵,第i行第j列表示第 i 个向量(当前词)对第 j 个向量的注意力分数
换句话说:
- 第 i 行:固定了一个 Query 向量(当前词)
- 这一行的所有列,就是它对每个 Key 向量(整个序列中所有词)的“相关性分数”
3️⃣ 缩放(Scaling)
为避免数值过大导致梯度不稳定,将结果除以维度平方根:
4️⃣ Softmax 归一化
将每一行通过 softmax 转化为概率分布:
归一化后,权重之和为 1,表示注意力分布。
5️⃣ 加权求和(信息聚合)
利用注意力权重矩阵 (A) 对 Value 向量加权求和:
其中:
- :第 i 个向量对第 j 个向量的关注权重
- :被关注的特征信息
- :新的上下文特征
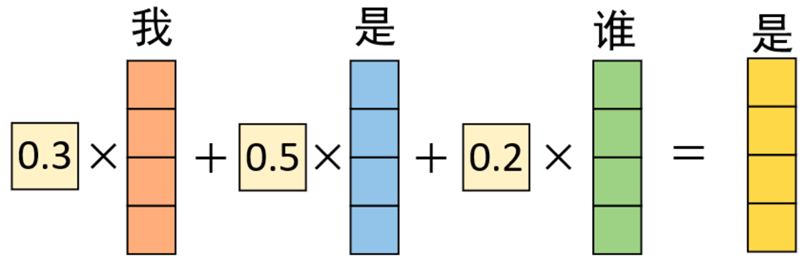
计算得到权重矩阵后,再将其作用于V得到最终的编码输出,如下图所示。
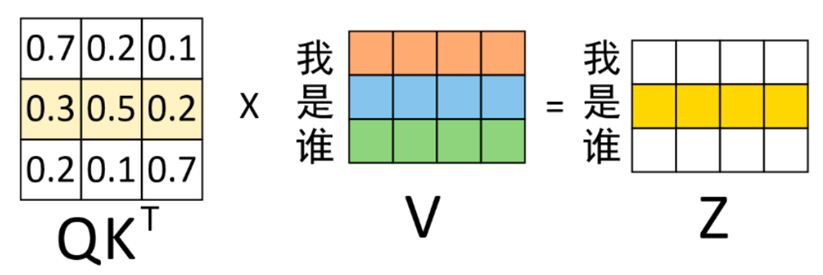
第1行中,0.7表示“我”与“我”的注意力值;0.2 表示“我”与“是”的注意力值;0.1表示“我”与“谁”的注意力值。在对序列中的“我”进行编码时,应将0.7的注意力放在“我”上,0.2注意力放在“是”上,将0.1注意力放在谁上。
3.完整公式
4.多头注意力(Multi-Head Attention)
模型在对当前位置的信息进行编码时,会过度的将注意力集中于自身的位置,因此作者提出了通过多头注意力机制来解决这一问题。同时,使用多头注意力机制还能够给予注意力层的输出包含有不同子空间中的编码表示信息,从而增强模型的表达能力。
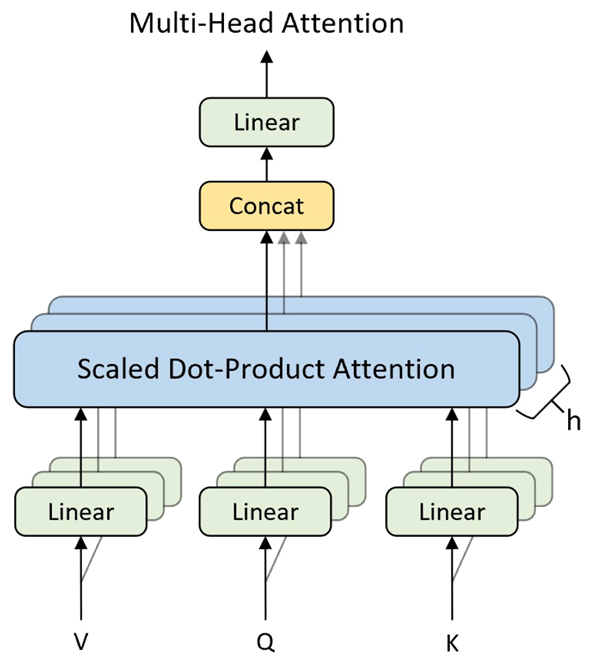
为了让模型学习多种“关注模式”,自注意力通常使用多头机制:
拼接各头结果:
每个注意力头可捕捉不同的语义、结构或位置相关性。
在论文中,作者使用了h=8个并行的自注意力模块来构建一个注意力层,对于每个自注意力模块限定了。这里可以发现,多头注意力机制是将一个大的高维单头拆分成了h个多头。因此,整个多头注意力机制计算过程可以通过如图所示来进行表示。
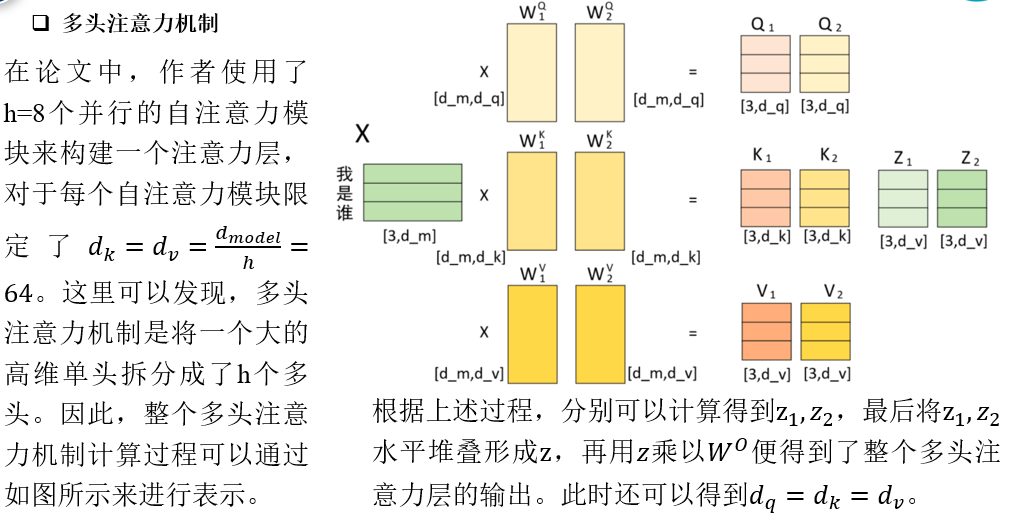
当输入维度相同,为什么还要用多个头?
单头不也能算出注意力吗?
单头的特点:
- 所有信息都压缩在一个“相关性空间”中;
- 这个头只能学习一种类型的关系模式。
例如:
只能捕捉 “语义相似性”,
但可能无法同时关注 “句法依赖” 或 “时序关联”。
多头注意力:
- 不要让一个头干所有事
- 我们可以用多个“小注意力头”,让它们分别学习不同的关系特征。
相同维度下多头与单头的区别:
假设模型总维度
- 单头:
每个 Q, K, V 向量维度都是 512。 - 多头(例如 8 头):
每个头使用较小维度 。
最终各头输出拼接回 512 维。
这意味着每个头学习一个不同的线性投影子空间。
因此:
多头注意力 ≈ 把输入向量分到不同的低维子空间中,
各自计算注意力,捕捉不同的语义关系。
假设总维度相同:
| 特性 | 单头 | 多头(相同总维度) |
|---|---|---|
| 维度分配 | 所有维度在一个空间 | 划分为多个子空间 |
| 表达能力 | 单一关注模式 | 多种关注模式并行 |
| 特征解耦 | 混合所有信息 | 不同头可学习不同特征 |
| 泛化能力 | 容易陷入某一模式 | 头之间多样化增强鲁棒性 |
当模型的维度确定时,一定程度上ℎ越大,整个模型的表达能力就越强,越能提高模型对于注意力权重的合理分配。
可视化理解:
想象输入矩阵为 512 维向量:
1 | |
每个小块(头)专注于不同“视角”,最终拼回完整表达。
总体对比:
| 对比维度 | 单头注意力 | 多头注意力(相同总维度) |
|---|---|---|
| 参数规模 | 相似 | 相似 |
| 学习空间 | 一个高维空间 | 多个低维子空间 |
| 学习到的关系类型 | 单一 | 多样 |
| 特征表达能力 | 较弱 | 更强 |
| 泛化与鲁棒性 | 一般 | 更好 |
5.计算流程概览
| 阶段 | 操作 | 含义 |
|---|---|---|
| 输入 | X | 一组向量 |
| 映射 | Q, K, V | 三种角色:查询、键、值 |
| 点积 | QKᵀ | 计算两两相关性 |
| Softmax | 归一化为注意力权重 | |
| 加权求和 | A·V | 按关注度聚合信息 |
| 输出 | Z | 融合上下文的新特征 |
2.位置编码(Positional Encoding)
2.1位置编码的基本思想
因为自注意力机制在实际运算过程中只是若干个矩阵进行线性变换。 因此即使打乱各个词的顺序,那么最终计算得到的结果本质上却没有发生任何变换,只是交换了对应的位置,但在实际情况中交换位置表达的含义也就不同。如图所示:

自注意力不感知顺序信息,因此需要加上位置编码(Positional Encoding):
-
表示词本身的含义
-
:表示词在序列中的位置
常见类型:
- 正弦 / 余弦编码(Transformer 原始版本)
- 可学习位置编码(BERT)
- 相对位置偏置(T5、DeBERTa)
2.2位置编码示例
如图所示,横坐标表示输入序列中的每个Token,每条曲线或直线表示对应Token在该维度上对应的位置信息。图中每个维度所对应的位置信息都是一个不变的常数;而右图中,每个维度所对应的位置信息均为基于某个公式变换得到的。换句话说就是,左图中任意两个 Token 上的向量都可以 进行位置交换而模型却不能捕捉到这一差异,但是加入右图这样的位置信息模型却能够感知到。
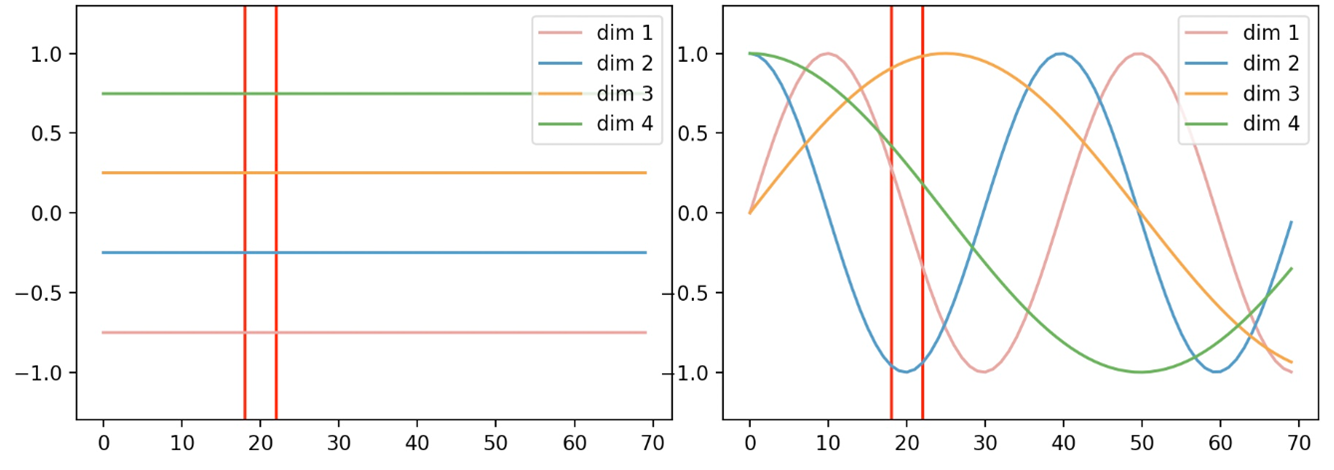
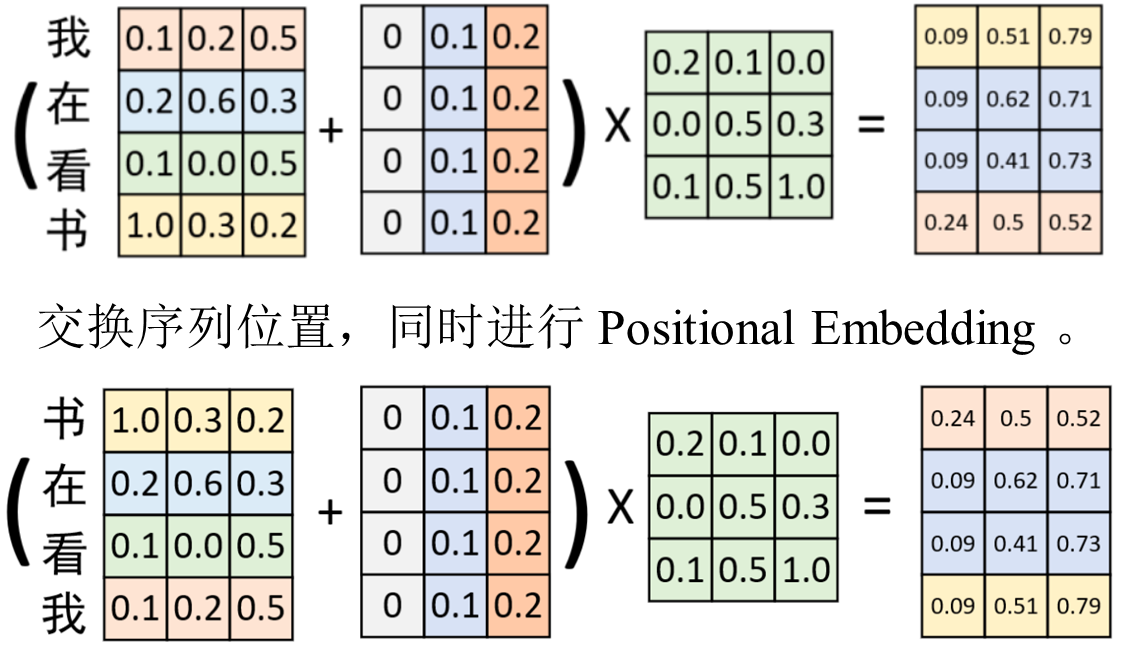
如图所示,原始输入Token Embedding后,又加入了一个常数位置信息的Positional Embedding。在经过一次线性变换后便得到了下图右边所示的结果。
在交换序列位置后,采用同样的Positional Embedding进行处 理,并进行线性变换。可以发现,其结果同之前的计算结果本质上没有发生变换。因此,这再次证明,如果Positional Embedding中位置信息是 以常数形式进行变换,那么这样的 Positional Embedding是无效的。
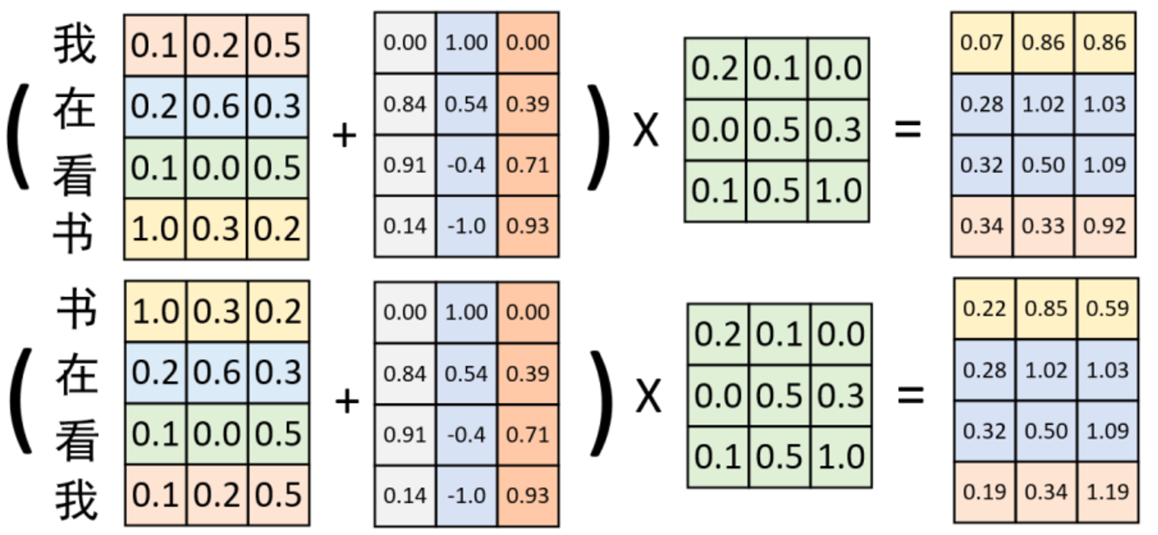
在融入非常数的 Positional Embedding 位置信息后,便可以得到如图所示的对比结果。在交换位置前后,与同一个权重矩阵进行线性变换后的结果截然不同。因此,这证明通过Positional Embedding可以弥补自注意力机制不能捕捉序列时序信息的缺陷
在Transformer中,作者采用了如下公式来生成各个维度的位置信息,其可视化结果如下图所示。
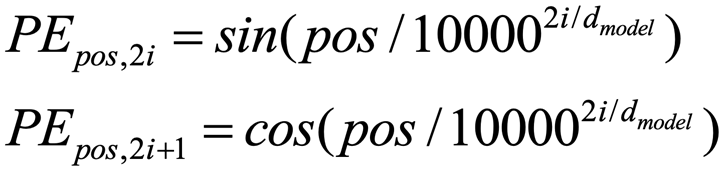
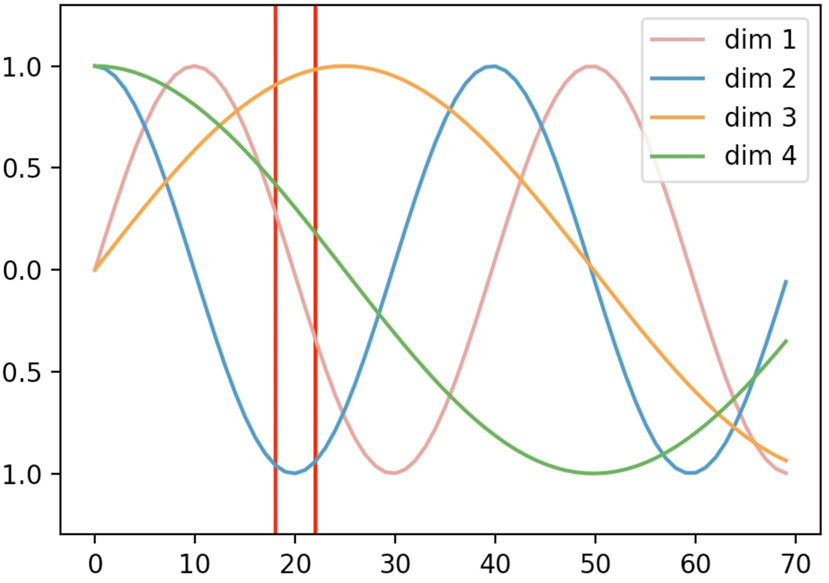
其中对应Positional Embedding矩阵,表示具体的某一个位置(行), 表示具体某一维度。
3.与其他网络结构的比较
| 对比项 | CNN | Self-Attention | RNN |
|---|---|---|---|
| 感受野 | 固定卷积核 | 可学习的全局关联 | 逐步传播 |
| 依赖建模 | 局部 | 全局 | 时间顺序依赖 |
| 并行性 | 高 | 高 | 低 |
| 长程依赖 | 弱 | 强 | 较弱 |
9.公式总结
🔗 参考资料
-
Vaswani et al., Attention Is All You Need, NeurIPS 2017
-
王成、黄晓辉《跟我一起学深度学习》
-
李宏毅老师课程:Self-Attention 讲解视频
总结:
自注意力通过学习不同向量之间的“相关性”,让模型能全局建模上下文关系。
它是 Transformer、BERT、ViT 等模型的核心基础结构。