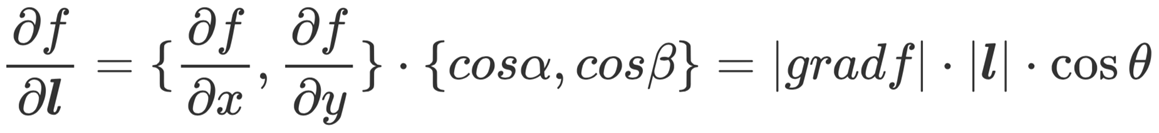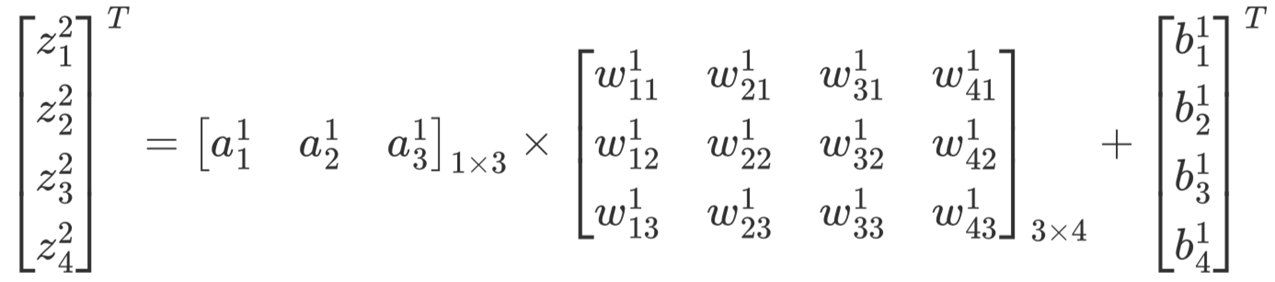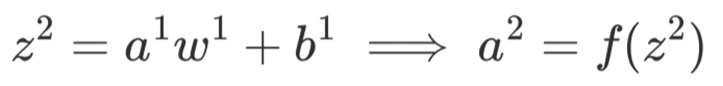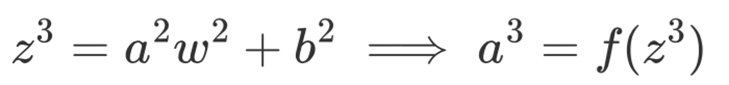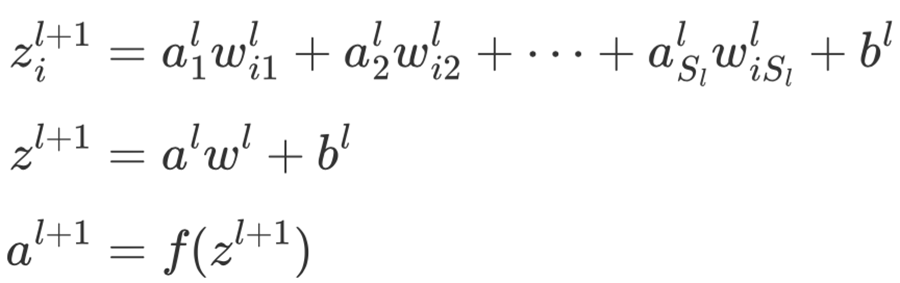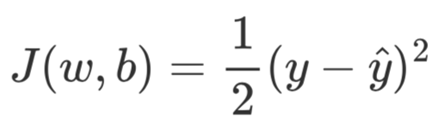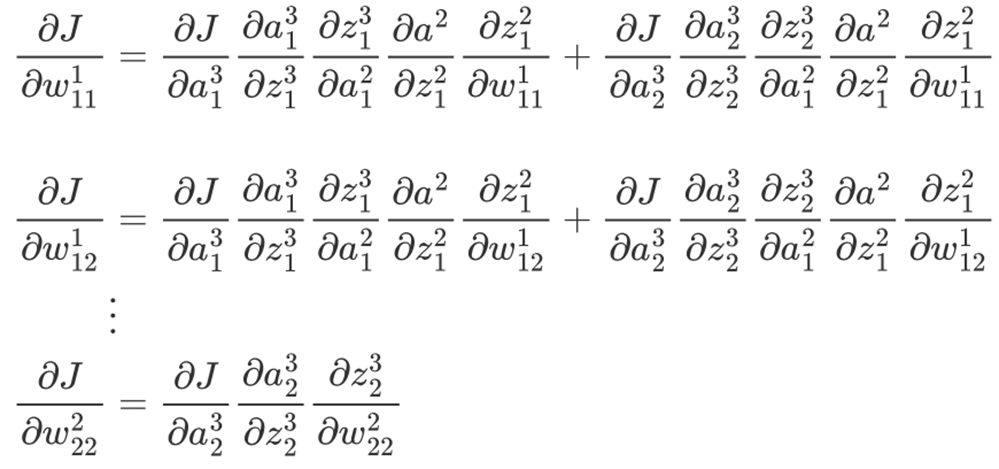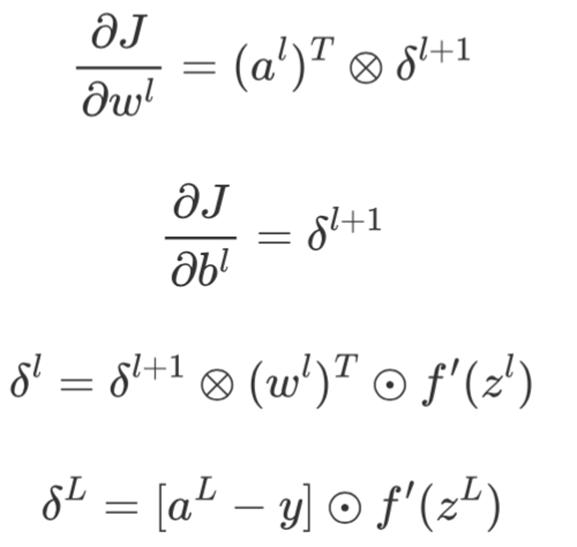梯度下降与反向传播

线性回归刚好是一个很简单的优化问题。与我们将在本书中所讲到的其他大部分模型不同，线性回归的解可以用一个公式简单地表达出来，这类解叫作解析解。像线性回归这样的简单问题存在解析解，但并不是所有的问题都存在解析解。解析解可以进行很好的数学分析，但解析解对问题的限制很严格，导致它无法广泛应用在深度学习里。即使在我们无法得到解析解的情况下，我们仍然可以有效地训练模型。在许多任务上，那些难以优化的模型效果要更好。因此，弄清楚如何训练这些难以优化的模型是非常重要的。本文中，我们用到一种名为梯度下降（gradient descent）的方法，这种方法几乎可以优化所有深度学习模型。它通过不断地在损失函数递减的方向上更新参数来降低误差。

1.梯度下降

梯度下降（Gradient Descent）是一种优化算法，用于最小化损失函数 $L(\theta)$ 。

核心思想是：沿着损失函数下降最快的方向（负梯度方向）更新参数。

θ←θ−\eta\frac{\partial L}{\partial \theta}

其中：

$L$ ：损失函数
$\eta$ ：学习率
$\frac{\partial L}{\partial \theta}$ ：梯度，表示参数对损失的影响程度

所以,梯度的大小直接决定了参数更新的速度和方向。

梯度下降算法的目的是用来最小化目标函数，也就是说梯度下降算法是一个求解的工具。当目标函数取到（或接近）全局最小值时，我们也就求解得到了模型所对应的参数。不过那什么又是梯度下降（Gradient Descent）呢？

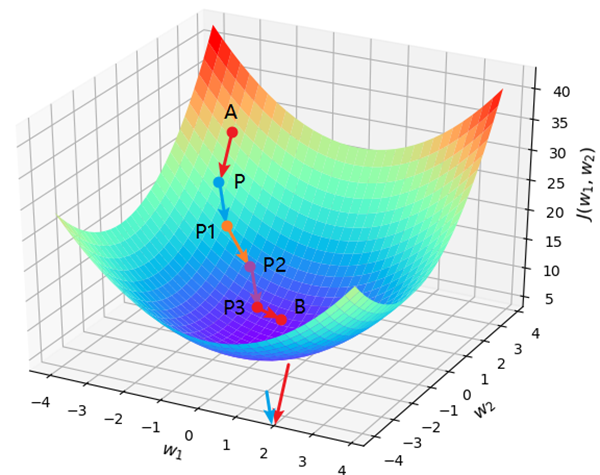
如图所示，假设有一个山谷，并且你此时处于位置A处，那么请问以什么样的方向（角度）往前跳，你才能最快地到达谷底B处呢?

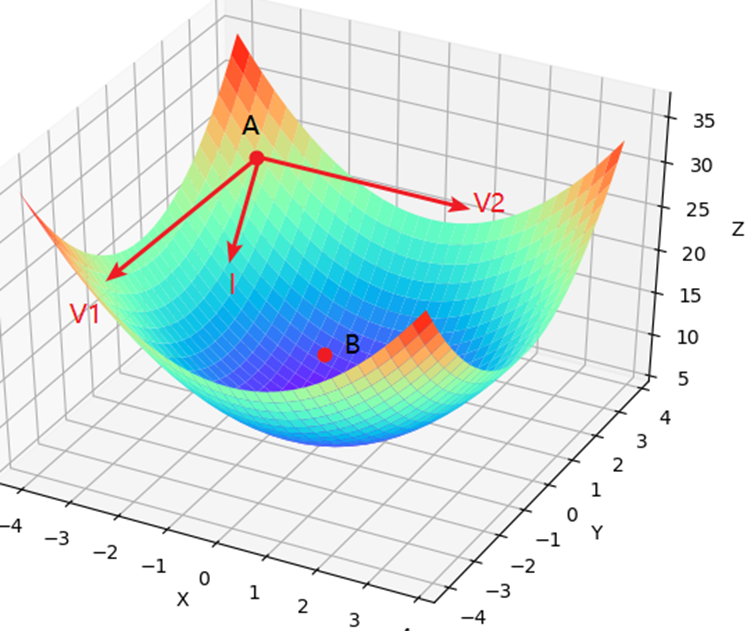
1.1 方向导数与梯度

函数 $f(x)$ 在 $x_0$ 处的导数反映的是 $f(x)$ 在 $x=x_0$ 处时的变化率； $f^′ (x_0)$ 越大，也就意味着 $f(x)$ 在该处的变化率越大，即移动 $Δx$ 后产生的函数增量 $Δy$ 越大。同理，在二元函数 $z=f(x,y)$ 中，为了寻找 $z$ 在 $A$ 处的最大变化率，就应该计算函数 $z$ 在该点的方向导数。

方向导数

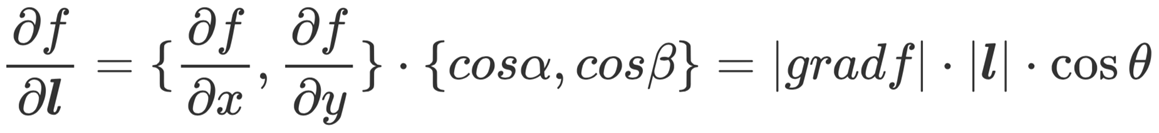
其中：

$l$ 为单位向量；
$α$ 为 $l$ 与 $x$ 轴的夹角
$β$ 为 $l$ 和 $y$ 轴的夹角
$θ$ 为梯度方向与 $l$ 的夹角

要想方向导数取得最大值，那么 $θ$ 必须为 $0$ ，由此可得，只有当某点方向导数的方向和梯度的方向一致时方向导数才能在该点取得最大变化率。

因此，要想每次都能以最快的速度下降，则每次都必须向着梯度的反方向向前跳跃。

1.2 梯度下降原理

现在有一个模型的目标函数 $J(w_1,w_2 )=w_1^2+w_2^2+2w_2+5$ ，其中 $w_1$ 和 $w_2$ 为待求解的权重参数，并且随机初始化点A为初始权重值。

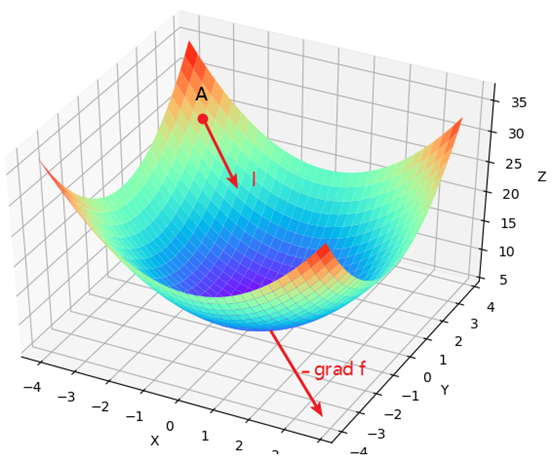
$OQ$ 为平面上梯度的反方向， $AP$ 为其平移后的方向，但是长度为之前的 $α$ 倍，因此，根据梯度下降的原则，此时曲面上的A点就该沿着其梯度的反方向跳跃，而投影到平面则为A应该沿着AP的方向移动。假定曲面上从A点跳跃到了P点，那么对应在投影平面上就是图中的AP部分，同时权重参数也从A的位置更新到了P点的位置。

可以看出向量 $AP 、 OA和OP$ 三者的关系为:

$OP=OA-PA$

进一步写为：

$OP=OA-α·grand J$

又由于 $OP$ 和 $OA$ 本质上是权重参数 $w_1$ 和 $w_2$ 更新后与更新前的值，所以便可以得出梯度下降的更新公式为:

w=w−α\frac{\partial J}{\partial w}

其中， $w=(w_1,w_2)$ ， $\frac{\partial J}{\partial w}$ 为权重梯度方向； $α$ 为步长用来放缩每次向前跳跃的距离，即学习率（Learning Rate）参数。

一步一步迭代更新，当A跳跃到P之后，又可以再次利用梯度下降算法进行跳跃，直到跳到谷底（或附近）为止，如图所示。

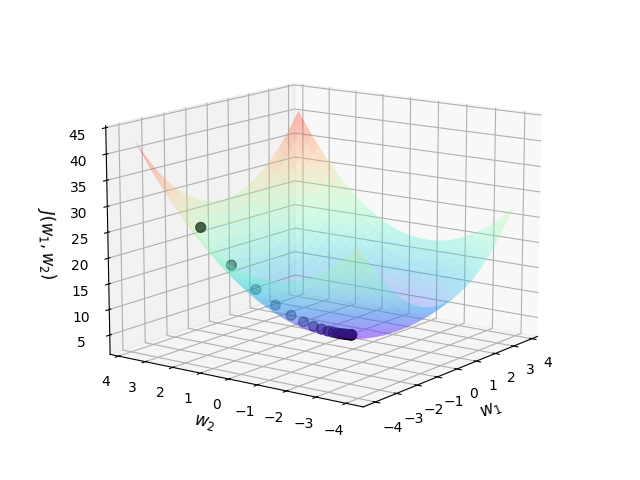
这里示例求解的是定义的目标函数对权重的梯度。

在深度学习中，我们一般求解的是损失函数关于模型参数（权重和偏执）的梯度。因为在深度学习中，损失函数衡量的是模型预测的准确程度，损失函数越小模型预测越准确。因此我们在学习过程中要使损失函数达到最小，而梯度下降就是求解的就是最小化问题，此时“目标函数 = 损失函数”

1.3 梯度下降的数学推导

假设有一个简单的线性模型：

\hat{y} = w x + b

损失函数（均方误差）为：

L(w, b) = \frac{1}{2n} \sum_{i=1}^n (\hat{y}_i - y_i)^2

梯度分别为：

\frac{\partial L}{\partial w} = \frac{1}{n} \sum_{i=1}^n (w x_i + b - y_i) x_i

\frac{\partial L}{\partial b} = \frac{1}{n} \sum_{i=1}^n (w x_i + b - y_i)

更新公式：

w \leftarrow w - \eta \frac{\partial L}{\partial w}, \quad b \leftarrow b - \eta \frac{\partial L}{\partial b}

1.4 梯度下降代码实现

from matplotlib import pyplot as plt
import numpy as np
from mpl_toolkits.mplot3d import Axes3D


def cost_function(w1, w2):
    J = w1 ** 2 + w2 ** 2 + 2 * w2 + 5
    return J


def compute_gradient(w1, w2):
    return [2 * w1, 2 * w2 + 2]


def gradient_descent():
    w1, w2 = -2, 3
    jump_points = [[w1, w2]]
    costs = [cost_function(w1, w2)]
    step = 0.1
    print("P:({},{})".format(w1, w2), end=' ')
    for i in range(20):
        gradients = compute_gradient(w1, w2)
        w1 = w1 - step * gradients[0]
        w2 = w2 - step * gradients[1]
        jump_points.append([w1, w2])
        costs.append(cost_function(w1, w2))
        print("P{}:({},{})".format(i + 1, round(w1, 3), round(w2, 3)), end=' ')
    return jump_points, costs


def plot_surface_and_jump_points(jump_points, costs):
    fig = plt.figure()
    ax = Axes3D(fig, auto_add_to_figure=False)
    fig.add_axes(ax)
    w1 = np.arange(-4, 4, 0.25)
    w2 = np.arange(-4, 4, 0.25)
    w1, w2 = np.meshgrid(w1, w2)
    J = w1 ** 2 + w2 ** 2 + 2 * w2 + 5

    ax.plot_surface(w1, w2, J, rstride=1, cstride=1,
                    alpha=0.3, cmap='rainbow')
    ax.set_zlabel(r'$J(w_1,w_2)$', fontsize=12)  # 坐标轴
    ax.set_ylabel(r'$w_2$', fontsize=12)
    ax.set_xlabel(r'$w_1$', fontsize=12)

    jump_points = np.array(jump_points)
    ax.scatter3D(jump_points[:, 0], jump_points[:, 1], costs, c='black', s=50)
    # jump_points[:, 0], jump_points[:, 1], costs 分别表示三维空间中X,Y,Z三个坐标
    plt.show()


if __name__ == '__main__':
    jump_points, costs = gradient_descent()
    plot_surface_and_jump_points(jump_points, costs)

梯度下降可视化图片

1.4. 三种基本变体

① 批量梯度下降（Batch Gradient Descent, BGD）

每次使用全部训练样本来计算梯度。

公式：

\theta \leftarrow \theta - \eta \frac{1}{n}\sum_{i=1}^{n}\nabla_{\theta}L_i(\theta)

优点：

收敛方向精确、稳定
缺点：
对大数据集计算量大、内存占用高
更新慢

适合：小数据集、线性回归、批量训练环境

② 随机梯度下降（Stochastic Gradient Descent, SGD）

每次只使用一个样本更新参数。

公式：

\theta \leftarrow \theta - \eta \nabla_{\theta}L_i(\theta)

优点：

计算快，每次迭代立即更新
有助于跳出局部极小值

缺点：

收敛波动大（更新方向噪声多）
需要较小学习率稳定训练

适合：在线学习（Online Learning）、大规模数据流

③ 小批量梯度下降（Mini-batch Gradient Descent）

每次使用一小批样本（batch）更新参数（最常用）。

公式：

\theta \leftarrow \theta - \eta \frac{1}{m}\sum_{i=1}^{m}\nabla_{\theta}L_i(\theta)

优点：

权衡计算效率与稳定性
支持 GPU 并行计算
是现代深度学习的默认选择

常见批量大小：32、64、128

import torch
from torch.utils.data import DataLoader, TensorDataset

# 假设我们有一些训练数据
x = torch.randn(1000, 2)
y = torch.randn(1000, 1)
dataset = TensorDataset(x, y)

# --- 小批量梯度下降 ---
batch_size = 32
loader = DataLoader(dataset, batch_size=batch_size, shuffle=True)

for epoch in range(5):
    for x_batch, y_batch in loader:
        # 计算预测与损失
        y_pred = model(x_batch)
        loss = loss_fn(y_pred, y_batch)

        # 反向传播 + 参数更新
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()

解释：

DataLoader 会随机打乱数据（shuffle=True）
每次从数据集中取出一个 batch（这里是 32 个样本）
每个 batch 都会执行一次 梯度下降更新

📌 这就是“小批量”和“随机性”的体现：

“小批量” → 每次只用一小部分样本计算梯度；
“随机” → 每次取样是随机的，不固定顺序。

BGD：每次都用全部1000个样本更新参数
SGD：每次只用1个样本更新
Mini-batch：每次用32个样本更新

1.5 带动量的梯度下降（Momentum）

思想：

在梯度更新中加入“惯性”概念，让优化方向更平滑、加速收敛。
相当于在参数更新中加入“速度项”。

公式：

v_t = \beta v_{t-1} + (1 - \beta)\nabla_{\theta}L(\theta_t)

\theta_{t+1} = \theta_t - \eta v_t

其中：

$v_t$ ：累积的梯度动量
$\beta$ ：动量系数（常取 0.9）

效果：

能加速在梯度方向一致的维度上的更新，减少震荡。

📈 直观理解：

在陡峭方向（梯度变化大）上平滑移动；
在平缓方向上积累“加速度”，快速向极小值前进。

2. 梯度消失和梯度爆炸

当然,也正是由于反向传播这一叠加累乘的计算特性为深度神经网络的训练过程埋下了两个潜在的隐患–梯度爆炸(Gradient Exploding)和梯度消失(Gradient Vanishing)。

对于梯度爆炸来讲通常是指模型在训练过程中网络的某一层或几层的梯度值过大,使梯度在反向传播时由于累乘的作用使越是靠近输入层的梯度越大,甚至超过了计算机能够处理的范围,从而导致模型的参数得不到更新。梯度爆炸通常是由于神经网络中存在的数值计算问题所导致的,例如网络的参数初始化不当、学习率设置过大等。为了避免产生梯度爆炸问题常见的方法有使用合适的参数初始化方法、调整学习率大小、使用梯度裁剪等。

对于梯度消失来讲则恰好与梯度爆炸相反,它是由于网络中的某一层或几层的梯度值过小,在梯度连续累乘的作用下将会得到一个非常小的梯度值,从而导致模型的参数无法得到有效更新。出现梯度消失的原因一般有参数初始化不当、使用不合适的激活函数及网络结构设计不合理等,常见的处理方法有选择合适的激活函数、使用批量归一化或者参数初始化方法等。

总结：

现象	描述
梯度消失	反向传播的梯度在层层相乘后趋近于 0，导致前面层几乎不更新。
梯度爆炸	梯度在层层相乘后指数级增大，导致参数剧烈震荡甚至变成 NaN。

问题	根本原因	现象	解决思路
梯度消失	导数 < 1 层层相乘	前层几乎不学习	ReLU、He初始化、BN、ResNet
梯度爆炸	导数 > 1 层层相乘	损失发散、NaN	梯度裁剪、权重正则、BN

表现：

梯度消失 → 学习停滞、模型训练极慢；
梯度爆炸 → 损失发散、参数变成 Inf 或 NaN。

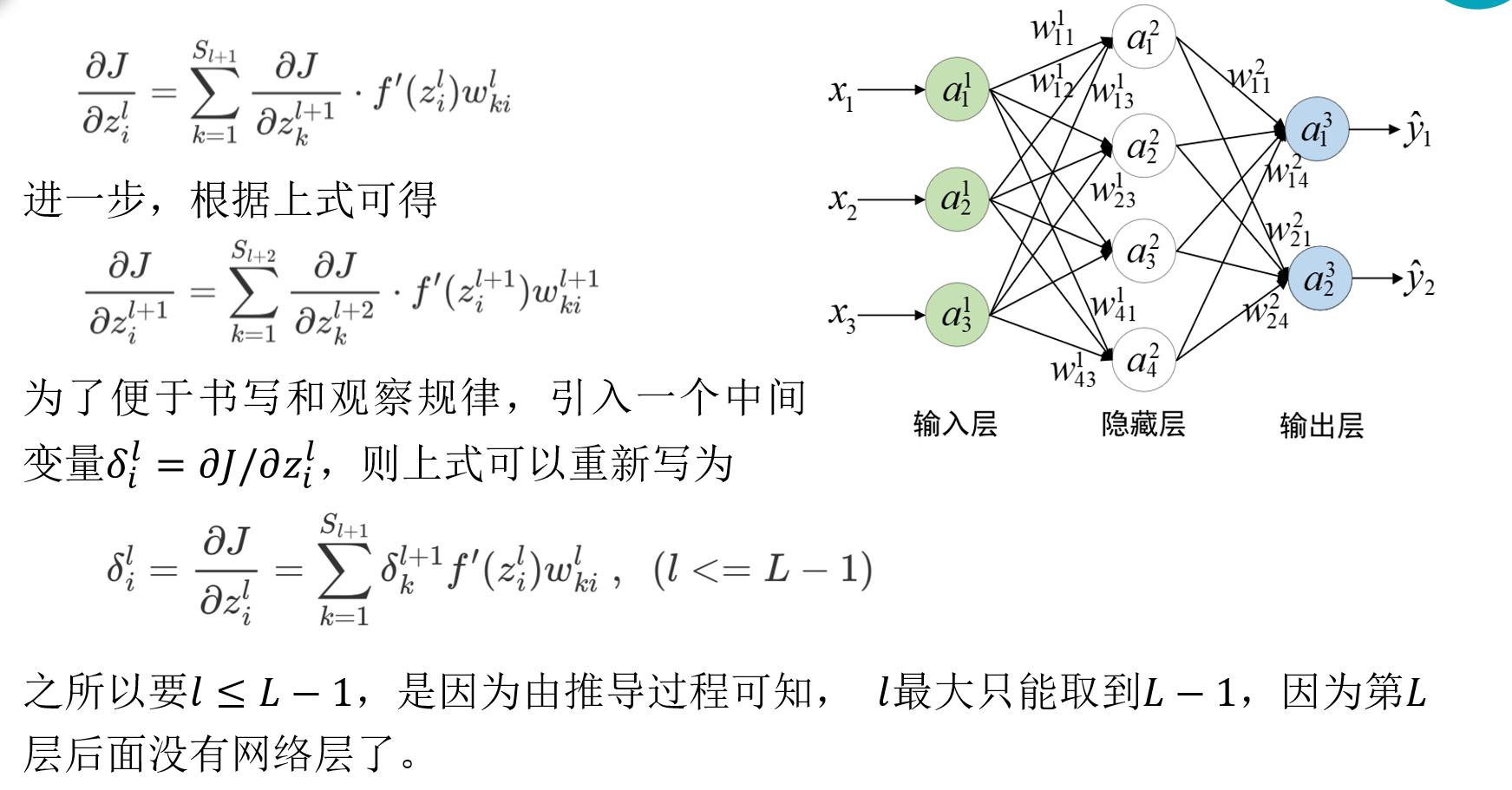
3.前向传播

定义：

$L$ 表示神经网络总共包含的层数, $S_l$ 表示第 $l$ 层的神经元数目， $K$ 表示输出层的神经元数目， $w_{ij}^l$ 表示第 $l$ 层第 $j$ 个神经元与第 $l+1$ 层第 $i$ 个神经元之间的权重值。

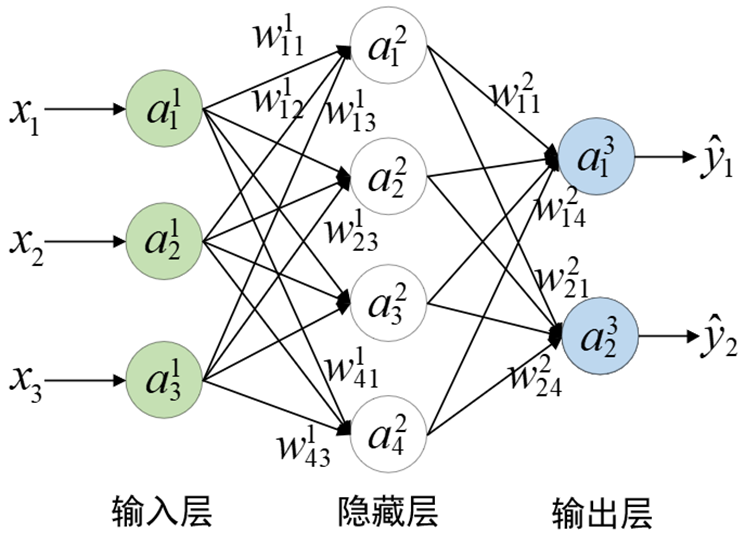
网络结构图

此时对于图所示的网络结构来说, $L=3,S_1=3， S_2=4,S_3=K=2$ ， $a_i^l$ 表示第 $l$ 层第 $i$ 个神经元的激活值（输入层 $a_i^1=x_i$ ),(输出层 $a_i^L=\hat{y_i}$ ）, $b_i^l$ 表示第 $l$ 层的第 $i$ 个偏置（未画出）。

计算过程：

第一层计算过程

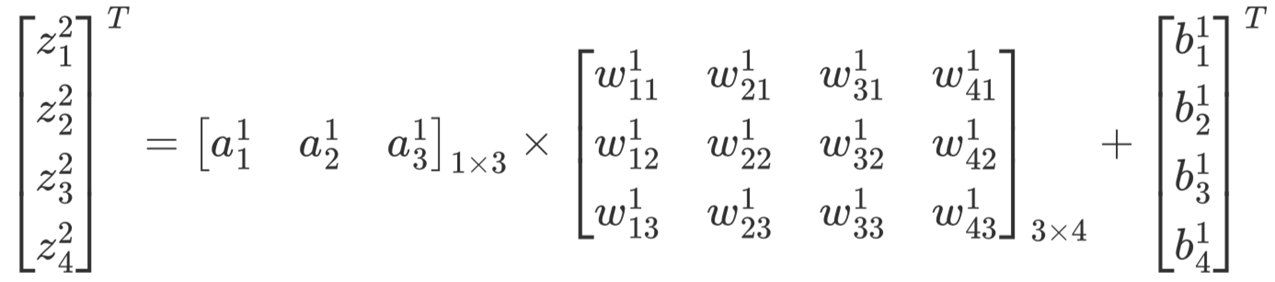
第一层：

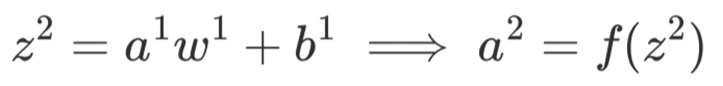
同理对于第2层来说有：

第2层

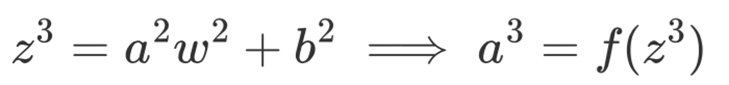
如果用一个通式进行表示的话则为：

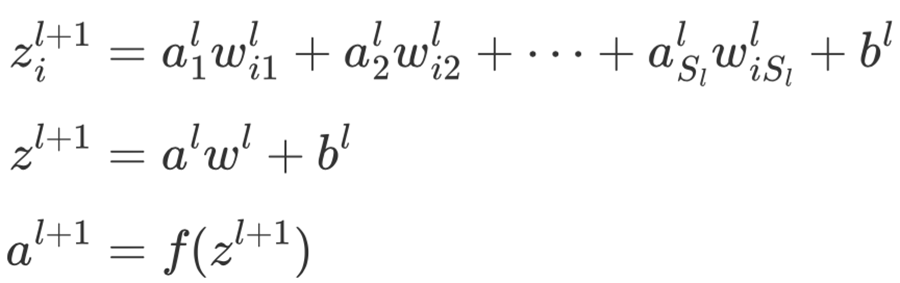
其中， $f(⋅)$ 表示激活函数，如 $Sigmoid$ 函数等。

上述整个计算过程，从输入到输出是根据从左到右按序计算而得到，因此，整个计算过程又被形象的叫做正向传播（Forward Propagation）或者是前向传播。

当训练得到权重 $w$ 之后便可以使用正向传播来进行预测了。进一步，再来看如何求解目标函数关于权重参数的梯度，以便通过梯度下降法求解网络参数。

4.反向传播

4.1 传统方式梯度求解

使用梯度下降求解模型参数的前提是要知道损失函数J关于权重的梯度，即J关于每个参数的偏导数。以下图网络结构为例，假设网络的目标函数为均方误差损失，且同时只考虑一个样本即

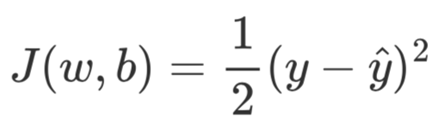
其中, $w$ 表示整个网络中的所有权重参数, $b$ 表示所有的偏置, $\hat{y}=a^3$ 。

网络结构图

符号	含义
$J$	损失函数 $Loss$
$a^l_i$	第 $l$ 层第 $i$ 个神经元的输出 $激活值$
$z^l_i$	第 $l$ 层第 $i$ 个神经元的输入（加权和）
$w^l_{ij}$	第 $l$ 层中从上一层第 $j$ 个节点到第 $i$ 个节点的权重
$\frac{\partial J}{\partial w^l_{ij}}$	损失函数对某个权重的偏导（我们最终要计算的梯度）

反向传播的本质：用链式法则把复杂的依赖关系拆解成一连串的局部导数相乘。

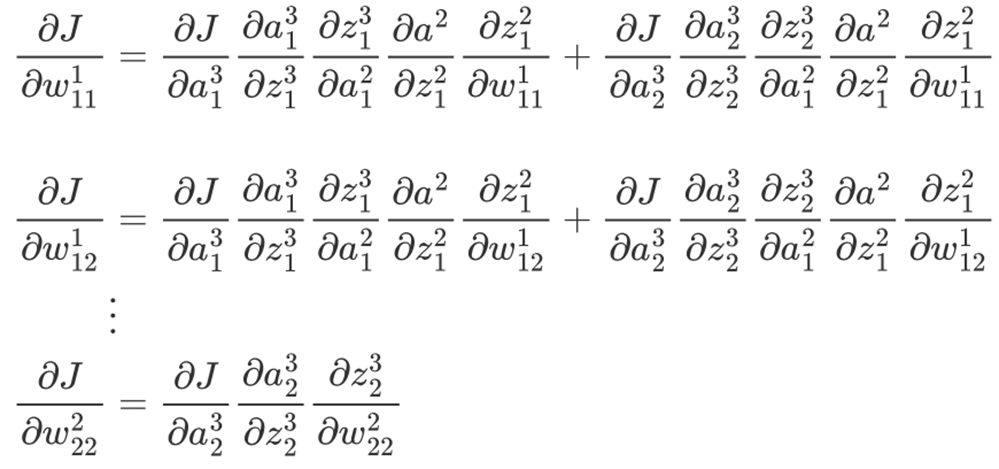
举个例子：

对于权重 $w_{11}^1$ （输入层到隐藏层的一个连接），损失 $J$ 依赖于它的路径是：

w_{11}^1 \rightarrow z_1^2 \rightarrow a_1^2 \rightarrow z_1^3, z_2^3 \rightarrow a_1^3, a_2^3 \rightarrow J

也就是说，这个权重影响隐藏层的第一个神经元输出 $a_1^2$ ，而 $a_1^2$ 又会影响输出层的两个节点 $a_1^3, a_2^3$ ，它们最终共同影响损失 $J$ 。

每个导数的含义：

局部导数	含义	说明
$\frac{\partial J}{\partial a_i^3}$	输出层的误差项	通常等于 $(\hat{y}_i - y_i)$
$\frac{\partial a_i^3}{\partial z_i^3}$	输出层激活函数的导数	若是线性激活 = 1
$\frac{\partial z_i^3}{\partial a_j^2}$	输出层加权输入对隐藏层输出的导数	就是 $w^2_{ij}$
$\frac{\partial a_j^2}{\partial z_j^2}$	隐藏层激活函数导数	$sigmoid′(z)$
$\frac{\partial z_j^2}{\partial w_{mn}^1}$	隐藏层线性输入对权重的导数	就是输入值 $a_n^1$

可以发现，整个计算过程做了很多重复计算，并且这还是网络相对简单的时候，对于深度学习中动则几十上百层的网络参数，这个过程便会无从下手。显然这种求解梯度的方式是不可取的，这也是为什么神经网络在一段时间发展缓慢的原因，就是因为没有一种高效的计算梯度的方式。

4.2 反向传播过程

经过矢量化后的形式为：

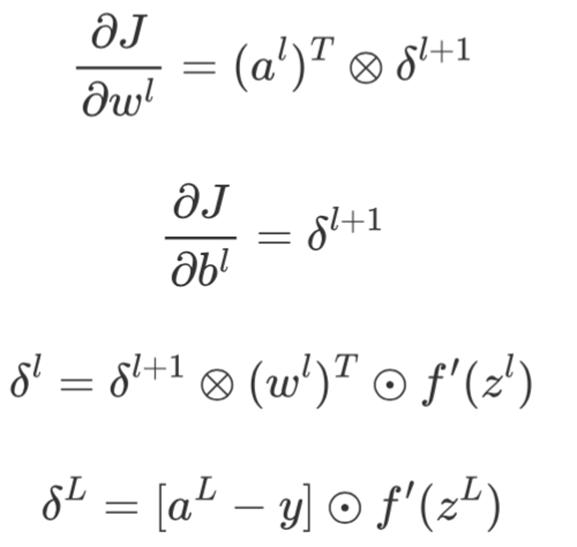
一个不争的事实：

1.最先求解出偏导数的参数一定位于第 $L-1$ 层上；

2.要想求解第l层参数的偏导数，一定会用到第 $l+1$ 层上的中间变量 $δ^{(l+1)}$ ；

3.整个过程是从右往左依次进行，所以又被形象地称为反向传播（Back Propagation），且 $δ^l$ 被称为第 $l$ 层的“残差”（Residual）。

在通过整个反向传播过程计算得到所有权重参数的梯度后，便可以根据梯度下降算法进行参数更新，而这两个计算过程对应的便是l.backward()和optimizer.step()这两个操作。

for data, target in dataloader:
    optimizer.zero_grad()      #  清空旧梯度
    output = model(data)       #  前向传播
    loss = criterion(output, target)  #  计算损失
    loss.backward()            #  反向传播，计算梯度
    optimizer.step()            #  梯度下降，更新参数

参考

王成、黄晓辉——《跟我一起学深度学习》

李沐——《动手学深度学习》

深度学习

#大模型 #深度学习

梯度下降与反向传播

https://this-is-kuo.github.io/2025/10/24/梯度下降与反向传播/

作者

Kuo

发布于

2025年10月24日

许可协议

逻辑回归到Softmax回归上一篇

线性回归下一篇