线性回归

1.线性回归模型

回归（regression）是能为一个或多个自变量与因变量之间关系建模的一类方法。 在自然科学和社会科学领域，回归经常用来表示输入和输出之间的关系。

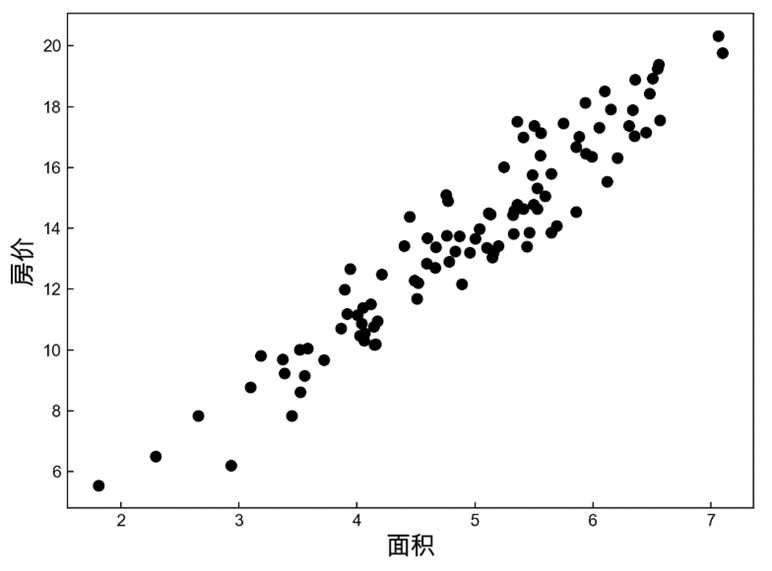
以房价预测为例， 我们希望根据房屋的面积（平方英尺）和房龄（年）来估算房屋价格（美元）。 为了开发一个能预测房价的模型，我们需要收集一个真实的数据集。 这个数据集包括了房屋的销售价格、面积和房龄。

在机器学习的术语中，该数据集称为训练数据集（training data set） 或训练集（training set）。 每行数据（比如一次房屋交易相对应的数据）称为样本（sample）， 也可以称为数据点（data point）或数据样本（data instance）。 我们把试图预测的目标（比如预测房屋价格）称为标签（label）或目标（target）。预测所依据的自变量（面积和房龄）称为特征（feature）或协变量（covariate）。

某些情况下，其它因素同样也能影响房屋价格。如到房屋学校、医院和到商场的距离等，所以这时便有了影响房价的4个因素，而在机器学习中将其称为特征（Feature）或属性（Attribute），因此，包含多个特征的线性回归就叫作多变量线性回归（Multiple Linear Regression）。

数学表达式为：

$$\hat{y} = w_1 x_1 + w_2 x_2 + \cdots + w_d x_d + b$$

或者用向量形式更简洁地表示：

$$\hat{y} = \mathbf{w}^\top \mathbf{x} + b$$

其中：

• $\mathbf{x} \in \mathbb{R}^d$：输入特征向量

• $\mathbf{w} \in \mathbb{R}^d$：权重参数,权重决定了每个特征对我们预测值的影响。

• $b \in \mathbb{R}$：偏置（bias）,偏置是指当所有特征都取值为0时，预测值应该为多少

• $\hat{y}$：预测值（prediction）

  

给定训练数据特征𝐗和对应的已知标签𝐲， 线性回归的目标是找到一组权重向量𝐰和偏置𝑏： 当给定从𝐗的同分布中取样的新样本特征时， 这组权重向量和偏置能够使得新样本预测标签的误差尽可能小。

虽然我们相信给定$\mathbf{x}$预测$y$的最佳模型会是线性的，但我们很难找到一个有$n$个样本的真实数据集，其中对于所有的$1 \leq i \leq n$，$y^{(i)}$完全等于$\mathbf{w}^\top \mathbf{x}^{(i)}+b$。无论我们使用什么手段来观察特征$\mathbf{X}$和标签$\mathbf{y}$，
都可能会出现少量的观测误差。因此，即使确信特征与标签的潜在关系是线性的，我们也会加入一个噪声项来考虑观测误差带来的影响。

在开始寻找最好的模型参数（model parameters）$𝐰$和$𝑏$之前， 我们还需要两个东西：

（1）一种模型质量的度量方式；

（2）一种能够更新模型以提高模型预测质量的方法。

---

2.损失函数

在我们开始考虑如何用模型拟合（fit）数据之前，我们需要确定一个拟合程度的度量。在线性回归中，我们的目标是让预测值尽可能接近真实值。但是「接近」这个概念需要量化 ——因此我们需要一个数学指标来衡量模型预测的“好坏”，这就是损失函数（Loss Function）。

损失函数越小，说明模型预测越准确。
学习过程 = 不断调整参数，使损失函数最小化。

2.1均方误差

回归问题中最常用的损失函数是平方误差函数。当样本$i$的预测值为$\hat{y}^{(i)}$，其相应的真实标签为$y^{(i)}$时，平方误差可以定义为以下公式：

单个样本的损失：

$$\ell(\hat{y}, y) = \frac{1}{2}(\hat{y} - y)$$

其中：

$\hat{y}$：预测值

$y$：真实值

系数 $\frac{1}{2}$ 是为了求导时简化（导数中可以抵消 2）

所有样本的平均损失：

$$\mathcal{L}(w, b) = \frac{1}{n} \sum_{i=1}^{n} \frac{1}{2}(\hat{y}^{(i)} - y^{(i)})^2 = \frac{1}{2n}\sum_{i=1}^n \left( (\mathbf{w}^\top \mathbf{x}^{(i)} + b) - y^{(i)} \right)$$

其中：

$n$表示样本数量;

$x^{(i)}$是第i个样本为一个列向量；

$w$是模型参数（权重）也为一个列向量；

$y^{(i)}$是第i个房屋的真实价格；

y ̂^{(i)}是第i个房屋的预测价格。

当$L$取最小值时的w ̂和{ b ̂ }就是要求的目标参数。当$L$最小值意味着所有样本的预测值与真实值之间的误差（Error）最小。因此，如何求解模型$h(x)$的就转换成了最小化函数$L$，而$L$也叫作目标函s数（Objective Function）。

优缺点

优点：

• 平滑、连续、可微；
• 对误差有“放大效应”，有助于优化；
• 解析上容易推导梯度。

缺点：

• 对异常点敏感（误差平方放大效果明显）。

替代方案：

• MAE（平均绝对误差）：$|\hat{y}-y|$，鲁棒但不可导；
• Huber 损失：结合 MSE 与 MAE 的优点。

---

3.神经网络

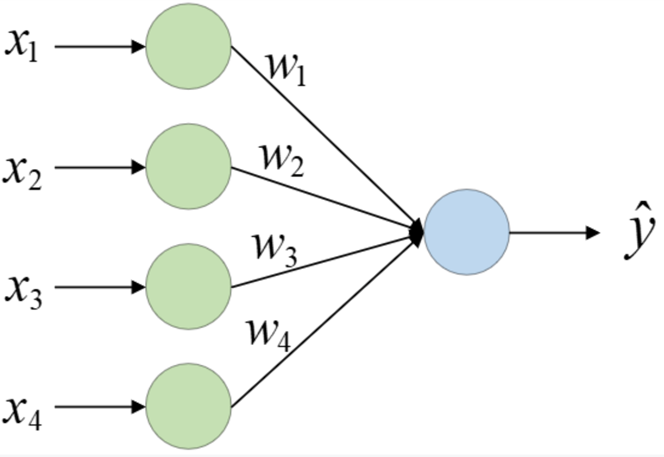
3.1单层神经网络

上面是一个简单的神经网络结构图，每个圈表示一个神经元（Neuron），输入层神经元个数表示样本特征维度，输出层神经元的个数表示输出维度。尽管这里有输入层(第0层）和输出层（第1层）两层，但在一般情况下只将含有参数（权重、偏置）的层称为一个网络层，因此线性回归模型是一个单层的神经网络。

图示的网络结构中，输出层和输入层的所有神经元都是完全连接的。如果某一层每个神经元的输入都完全依赖于上一层所有神经元的输出，则将该层称作是一个全连接层（Fully-connected Layer）。或者稠密层（Dense Layer）。上图的输出层就是一个全连接层。

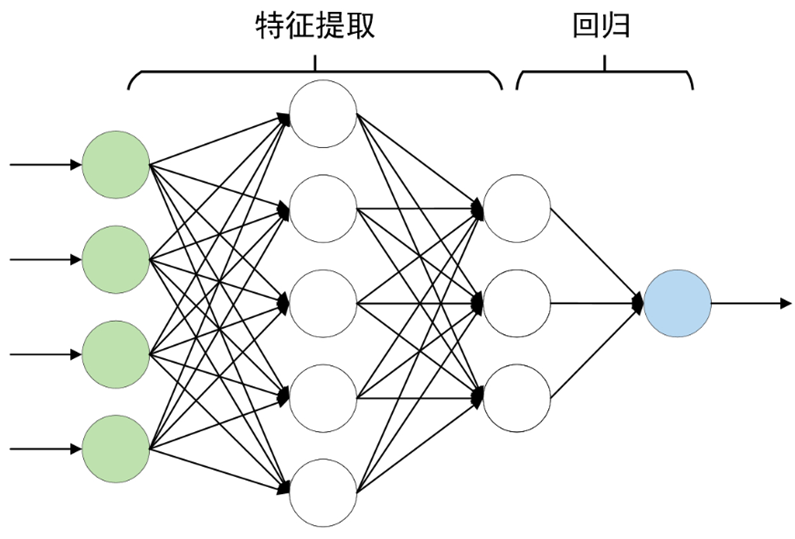
3.2深度神经网络

深度神经网络（Deep Neural Network, DNN）也叫做深度前馈神经网络（Deep Forward Neural Network）一般是指网络网络层数大于2的神经网络，如图所示便是一个简单的深度神经网络，其有3个全连接层。同时，将输入层与输出层之间的所有层都称为隐藏层或隐含层（Hidden Layer）。

对于输出层之前的所有层，都可以将其看成是一个特征提取的过程，而且越靠近输出层的隐含层也就意味着提取得到的特征越抽象。当原始输入经过多层网络的特征提取后，就可以将提取得到的特征输入到最后一层进行相应的操作（分类或者回归等）。

4.线性回归简洁实现

4.1 nn.Linear()使用

如图所示，对于每个网络层来说均是一个全连接层。例如对于第1个全连接层来说，其输入维度（神经元的数量）为4，输出维度为5，即由5个线性组合构成了该全连接层。同时nn.Linear()已经在内部随机初始化了网络层对应的权重参数。此时可以通过如下方式来定义该全连接层，示例代码如下所示：

import toprch.nn as nn
layer = nn.Linear(4,5)

第1行导入torch中的nn模块。第2行定义一个全连接层且nn.Linear()内部已经随机初始化了网络层对应的权重。同理对于第2个全连接层来说定义方式为nn.Linear(5, 3)。

通过如下方式来完成一次全连接层的计算，示例代码如下所示：

def test_linear():
	x = torch.tensor([[1.,2,3,4],[4,5,6,7]])
	layer = nn.Linear(4,5)
	y = layer(x)
	#1. 中的点是为了让数字变成浮点数，确保 PyTorch 张量是浮点类型

第2行表示定义输入样本，形状为[2,4]列，即样本数量为2，特征数量为4。第4行则是计算该全连接层对应的结果，输出形状为[2,5]。

4.2 nn.Sequential()使用

此时已经知道了如何定义一个全连接层，并完成计算，但图中有多个全连接层，此时可以将所有网络层放入到一个有序容器中一次完成整个计算过程，示例代码如下：

def multi_layers_sequential():
	x = torch.tensor([[1.,2,3,4],[5,6,7,8]], dtype=torch.float32)
	net = nn.Sequential(nn.Linear(4,5),nn.Linear(5,3),nn.Linear(3,1))
	y = net(x)
	print(y)

4.3 nn.MSELoss使用

在定义好一个模型之后便需要通过最小化对应的损失函数来求解得到模型对应的权重参数。在此处可以通过计算预测值与真实值之间的均方误差来构造损失函数。在PyTorch中，可以借助nn.MSELoss()来实现这一目的。

def test_loss():
	y = torch.tensor([1,2,3],dtype=torch.float32)
	y_hat = torch.tensor([2,2,1],dtype=torch.float32)
	l1 = 0.5 * torch.mean((y-y_hat)**2）
	
	loss = nn.MSELoss(reduction='mean')
	l2 = loss(y,y_hat)
	print(l1,l2)

第2-3行定义真实值和预测值这两个张量。第4行表示自行实现损失计算。第5~6行借助PyTorch中nn.MSELoss()来实现，其中reduction='mean’表示返回均值，而reduction='sum’表示返回和。

MSE 本身已经包含了“平方”和“平均”，不需要再乘以 0.5。只有在某些优化场景（如配合 L2 正则或特定梯度推导）中，才会使用 0.5 * MSE 来简化导数（因为平方的导数是 2x，乘 0.5 后变成 x），但此时也必须先平方再平均。

4.4房价预测实现

第6~7行表示将其转换为PyTorch中的张量，且指定类型为浮点型。第8行表示返回测试数据，两者的形状均为[100,1]。

import numpy as np
import torch
import torch.nn as nn
import matplotlib.pyplot as plt

"""
1.构建数据集
随机产生100个样本点并加入相应的噪声，其中x表示房屋面积，y表示房屋价格。

"""
def make_house_data():
    """
    构造数据集
    :return:  x:shape [100,1] y:shape [100,1]
    """
    np.random.seed(20)				 # 固定随机种子，确保每次运行生成相同数据，便于复现
    x = np.random.randn(100, 1) + 5  # 面积（100个样本），均值为5，标准差为1的正态分布
    noise = np.random.randn(100, 1)  # 噪声，标准正态分布
    y = x * 2.8 - noise  # 价格
    """
    表示将其转换为PyTorch中的张量，且指定类型为浮点型。
    """
    x = torch.tensor(x, dtype=torch.float32)
    y = torch.tensor(y, dtype=torch.float32)
    return x, y		#表示返回测试数据，两者的形状均为[100,1]。
	
    
    """
	可视化函数
	"""
def visualization(x, y, y_pred=None):
    plt.rcParams['ytick.direction'] = 'in'  # 刻度向内
    plt.rcParams['xtick.direction'] = 'in'  # 刻度向内
    plt.xlabel('面积', fontsize=15)		   #横纵坐标标签
    plt.ylabel('房价', fontsize=15)
    plt.scatter(x, y, c='black')	#对原始样本点可视化。散点图，真实数据
    # plt.rcParams['font.sans-serif'] = ['SimHei'] # 指定默认字体
    plt.plot(x, y_pred)		#预测结果可视化
    plt.rcParams['font.sans-serif'] = ['Arial Unicode MS']
    plt.tight_layout()  # 调整子图间距
    plt.show()			#展示绘图结果


def train(x, y):
    epochs = 40
    lr = 0.003
    input_node = x.shape[1]		#构建的特征输入输出维度为1
    output_node = 1
    net = nn.Sequential(nn.Linear(input_node, output_node)) #线性模型，全连接层，放入顺序容器中
    loss = nn.MSELoss()  # 定义损失函数
    """
    定义随机梯度下降优化器来求解模型，其中net.parameters()表示得到容器中所有网络层	对应的参数，lr表示执行梯度下降时的学习率。
    """
    optimizer = torch.optim.SGD(net.parameters(), lr=lr)  # 定义优化器，随机梯度下降
    """
    迭代求解网络中的权重参数，即训练过程。
    """
    for epoch in range(epochs):
        logits = net(x)				#前向传播
        l = loss(logits, y)			#计算损失
        optimizer.zero_grad()		#清空梯度
        l.backward()				#反向传播
        optimizer.step()  			# 执行梯度下降，更新参数
        print("Epoch: {}, loss: {}".format(epoch, l))
    #训练结束后再计算一次
    """
    则是根据训练完成的模型来对房价进行预测。
    """
    logits = net(x)
    l = loss(logits, y)
    print("RMSE: {}".format(torch.sqrt(l / 2)))
    return logits.detach().numpy()


if __name__ == '__main__':
    x, y = make_house_data()
    y_pred = train(x, y)
    visualization(x, y, y_pred)

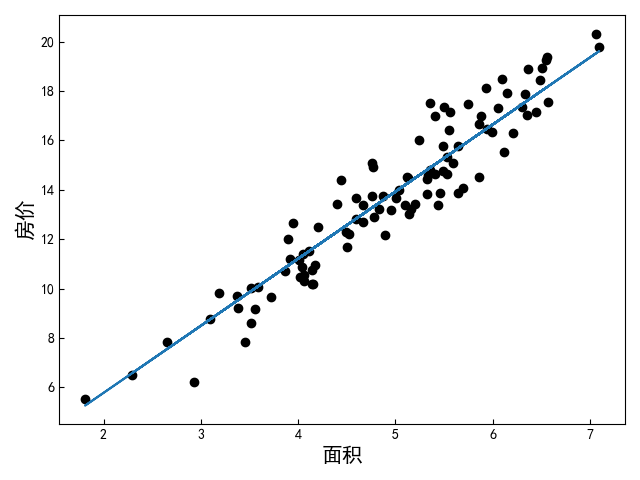
图中圆点表示原始样本，直线表示根据输入面积预测得到的结果

#日志
Epoch: 0, loss: 279.0893249511719
Epoch: 1, loss: 197.5123291015625
Epoch: 2, loss: 139.86776733398438
Epoch: 3, loss: 99.1345443725586
Epoch: 4, loss: 70.3512954711914
Epoch: 5, loss: 50.01227569580078
Epoch: 6, loss: 35.640159606933594
Epoch: 7, loss: 25.484416961669922
Epoch: 8, loss: 18.308088302612305
Epoch: 9, loss: 13.237091064453125
Epoch: 10, loss: 9.653782844543457
Epoch: 11, loss: 7.121710300445557
Epoch: 12, loss: 5.332477569580078
Epoch: 13, loss: 4.068147659301758
Epoch: 14, loss: 3.174736261367798
Epoch: 15, loss: 2.5434224605560303
Epoch: 16, loss: 2.097313642501831
Epoch: 17, loss: 1.7820767164230347
Epoch: 18, loss: 1.559316873550415
Epoch: 19, loss: 1.4019043445587158
Epoch: 20, loss: 1.2906664609909058
Epoch: 21, loss: 1.2120589017868042
Epoch: 22, loss: 1.1565083265304565
Epoch: 23, loss: 1.1172503232955933
Epoch: 24, loss: 1.0895051956176758
Epoch: 25, loss: 1.0698949098587036
Epoch: 26, loss: 1.0560336112976074
Epoch: 27, loss: 1.0462342500686646
Epoch: 28, loss: 1.039305329322815
Epoch: 29, loss: 1.0344047546386719
Epoch: 30, loss: 1.0309374332427979
Epoch: 31, loss: 1.0284826755523682
Epoch: 32, loss: 1.026743769645691
Epoch: 33, loss: 1.025510549545288
Epoch: 34, loss: 1.0246347188949585
Epoch: 35, loss: 1.024011492729187
Epoch: 36, loss: 1.023566484451294
Epoch: 37, loss: 1.0232475996017456
Epoch: 38, loss: 1.0230181217193604
Epoch: 39, loss: 1.0228509902954102
RMSE: 0.7150974869728088

参考

1.王成、黄晓辉《跟我一起学深度学习》

2.李沐-《动手学深度学习》