逻辑回归到Softmax回归

逻辑回归到Softmax回归

1.分类问题

一个新算法的诞生要么用来改善已有的算法模型，要么就是首次提出用来解决一类新的问题，而逻辑回归模型恰恰属于后者，它是用来解决一类新的问题——分类（Classification）。什么是分类问题呢？

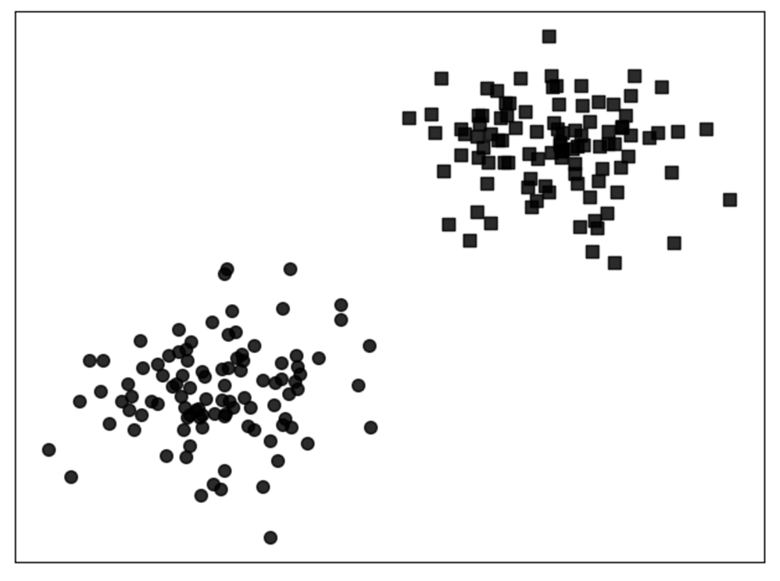
现在有两堆样本点，需要建立一个模型来对新输入的样本进行预测，判断其应该属于哪个类别，即二分类问题（Binary Classification），如图所示。线性回归解决不了，那么我们可不可以在此基础上做一点改进以实现分类的目的呢？

分类任务

2.逻辑回归模型

可以通过建立一个模型用来预测每个样本点(x1,y1)(x_1,y_1)属于其中一个类别的概率pp，如果p>0.5p>0.5就可以认为该样本点属于这个类别，这样就能解决上述的二分类问题了。该怎样建立这个模型呢？在线性回归中，我们的输出可能是任意实数，但此处既然要得出一个样本所属类别的概率最直接的办法就是，通过一个函数g(z)g(z) ，将x1x_1和x2x_2这两个特征的线性组合映射至［0,1］的范围。由此便得到了逻辑回归中的预测模型：

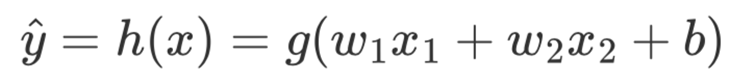
其中，g(⋅)g(⋅)同样为Sigmoid函数；w1,w2w_1,w_2和bb为未知参数；h(x)h(x)称为假设函数（Hypothesis），当h(x)h(x)大于某个值（通常设为0.5）时，便可以认为样本xx属于正类，反之则认为属于负类。同时，也将w1x1+w2x2+b=0w_1 x_1+w_2 x_2+b=0称为两个类别间的决策边界（Decision Boundary）。当求解得到w1,w2w_1,w_2和b后，也就意味着得到了这个分类模型。

如果该数据集有nn个特征维度，那么同样只需要将所有特征的线性组合映射至区间 [0,1] 即可

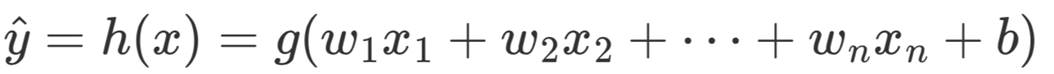
可以看出，逻辑回归本质上也是一个单层的神经网络。可以通过下方示意图来对上式中的模型进行表示。其中，输出层的曲线就表示这个映射函数g(z)g(z)。

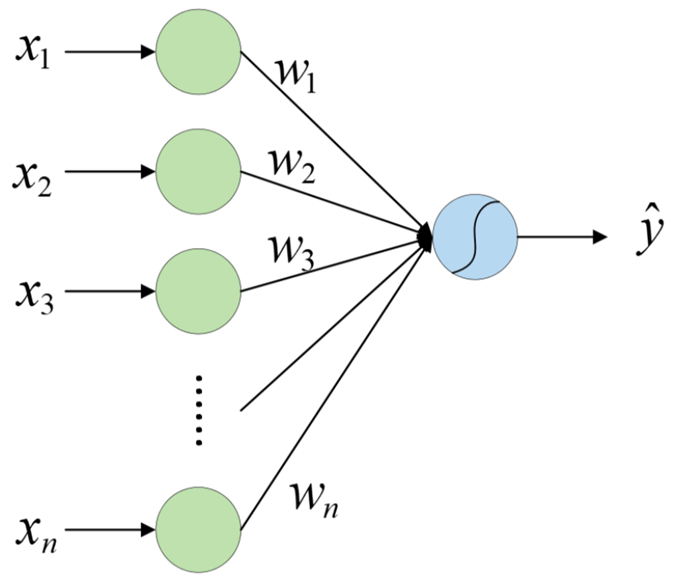
同线性回归一样也需要通过一种间接的方式，即通过目标函数来刻画预测标签（Label）与真实标签之间的差距。当最小化目标函数后，便可以得到需要求解的参数ww和bb 。对于逻辑回归来说可以通过最小化以下目标函数来求解模型参数

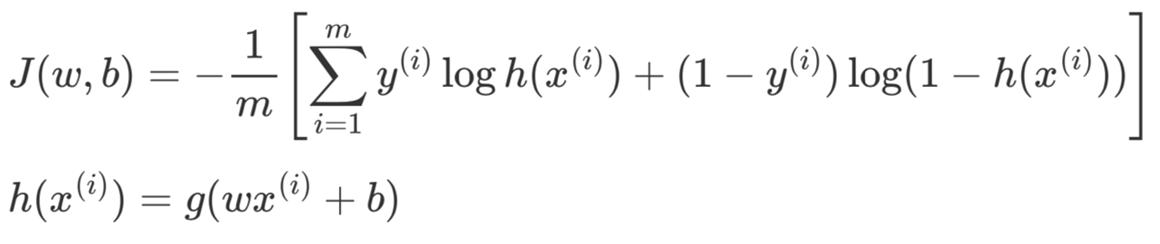
其中，mm表示样本总数， x(i)x^{(i)}表示第i个样本， y(i)y^{(i)}表示第ii个样本的真实标签，取值为0或1， h(x(i))h(x^{(i)}) 表示第ii个样本为正类的预测概率。当函数JJ取得最小值的参数w ̂和b ̂ ，也就是要求的目标参数。

3.从二分类到多分类

在实际情况中，绝大多数任务场景都不会是一个简单的二分类任务。通常情况下在用逻辑回归处理多分类任务时，都会采取一种称为One-vs-all（也叫作 One-vs-rest）的方法。

One-vs-all策略的核心思想是每次将其中一个类别的样本和剩余其它类的所有样本两者看作一个二分类任务进行模型训练，最后在预测过程中选择输出概率值最大那个模型对应的类别作为该样本点的所属类别。

图3.1

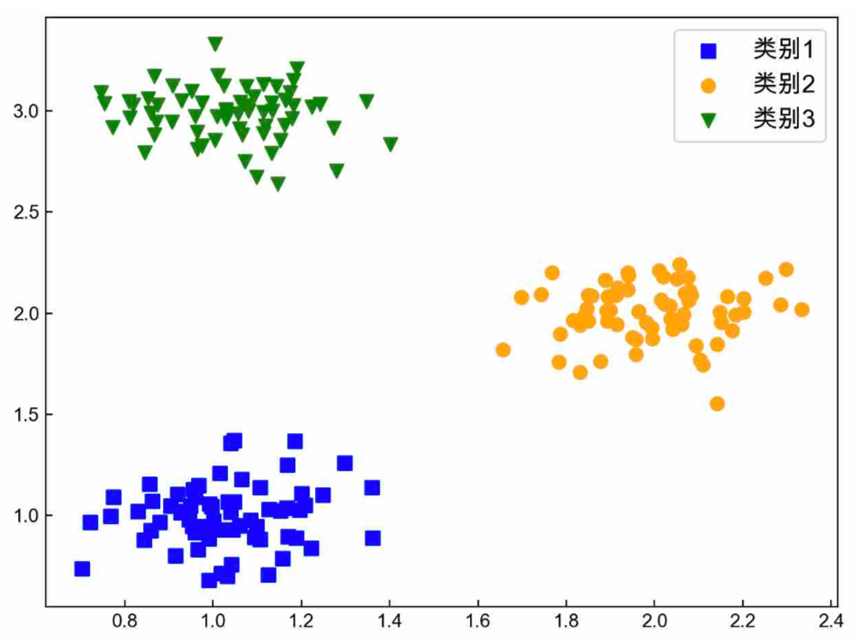
如图3.1为一个三分类的数据集，One-vs-all策略的核心是每次将其中一个类别的样本和剩余其它类的所有样本看作一个二分类任务进行模型训练如图3.2所示最后在预测过程中选择输出概率值最大的那个模型对应的类别作为该样本点的所属类别。

因此，可以建立3个二分类模型h1(x)h_1 (x)、h2(x)h_2 (x)和h3(x)h_3 (x)来完成整个3分类任务。

图3.2

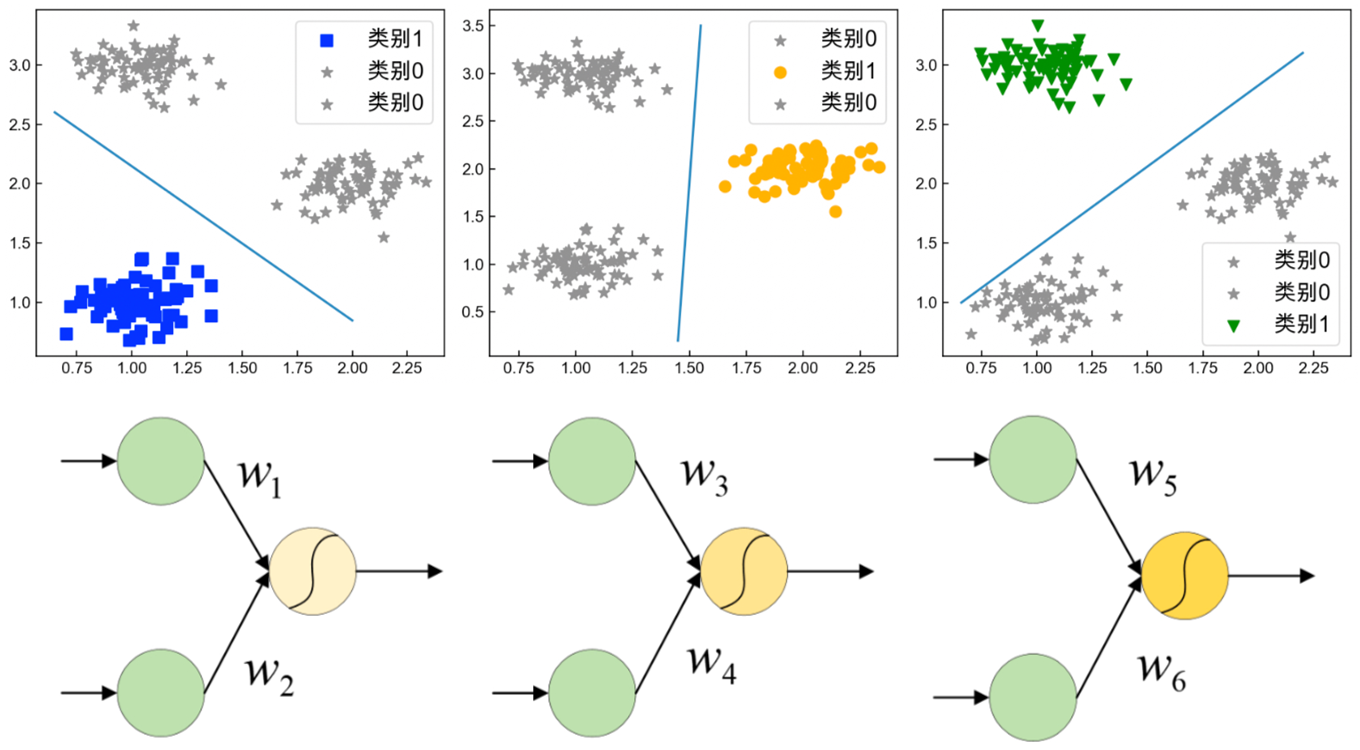
进一步可以简化为下图所示的形式。在这种条件下，模型训练时的标签将会被重新编码为另外一种形式。例如有5个样本，其类别编号分别为0、0、1、2、1，那么第1个样本的标签将被编码[1,0,0]；第2个为[1,0,0]；后续3个依次为[0,1,0]、[0,0,1]和[0,1,0]，以此来与上面的3个输出计算损失。这种编码在深度学习中被称为独热（One-hot）编码。

图3.3

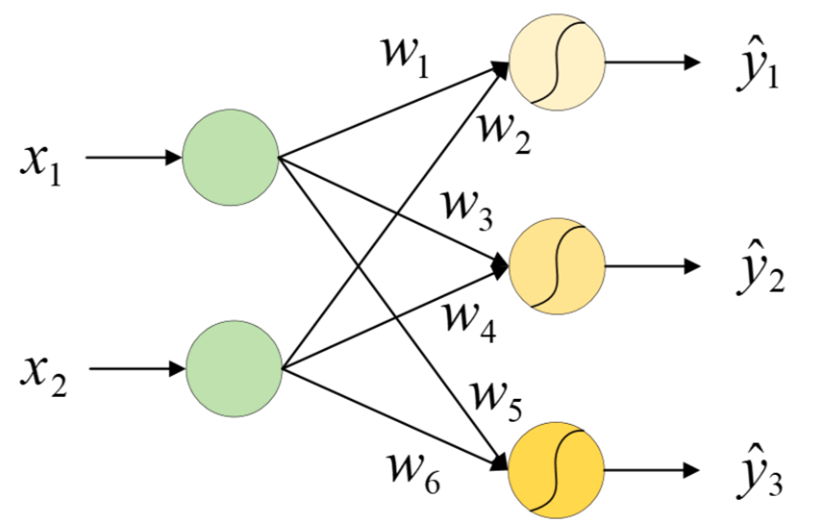
4.Softmax回归

要将输出视为概率，我们必须保证在任何数据上的输出都是非负的且总和为1。如果有一种方法将输出层的置信值进行归一化，使得大小关系不变但所有结果相加等于1，那么便可以将整个输出结果视为该样本属于各个类别的概率分布。例如将[0.8,0.7,0.9]归一化成[0.33,0.30,0.37]。Softmax函数就是这样做的。

softmax函数能够将未规范化的预测变换为非负数并且总和为1，同时让模型保持可导的性质。为了完成这一目标，我们首先对每个未规范化的预测求幂，这样可以确保输出非负。 为了确保最终输出的概率值总和为1，我们再让每个求幂后的结果除以它们的总和。如下式：

y^=softmax(o)其中y^j=exp⁡(oj)∑kexp⁡(ok)\hat{\mathbf{y}} = \mathrm{softmax}(\mathbf{o})\quad \text{其中}\quad \hat{y}_j = \frac{\exp(o_j)}{\sum_k \exp(o_k)}

同逻辑回归一样，对于图3.1中的三分类模型来说，Softmax回归首先进行各个特征之间的线性组合，然后再归一化处理。

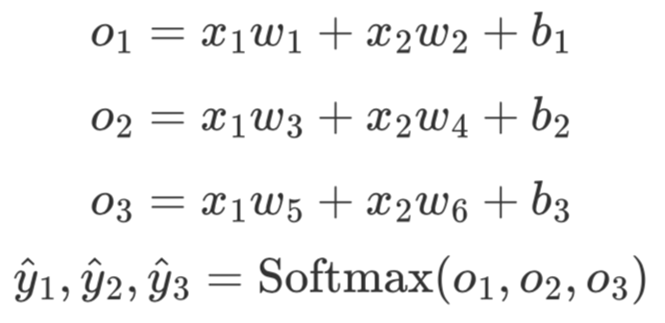
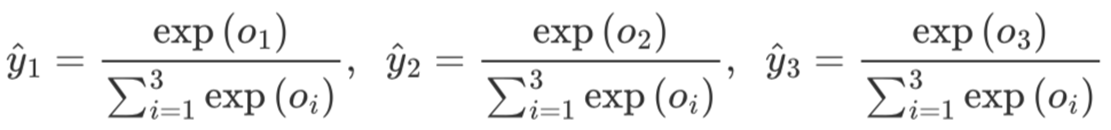
在经过，归一化过程后，可以看出y1^+y2^+y3^=1\hat{y_1}+\hat{y_2}+\hat{y_3}=1,并且0<y1^，y2^，y3^<10<\hat{y_1}，\hat{y_2}，\hat{y_3}<1，即y1^，y2^，y3^\hat{y_1}，\hat{y_2}，\hat{y_3}是一个合法的概率分布。最后通过不同类别的输出概率值的大小便能判断每个样本的所属类别。

交叉熵损失（损失函数-对数似然）

对于多分类任务来说可以通过衡量两个概率分布之间的相似性，即交叉熵（Cross Entropy）来构建目标函数，并通过梯度下降算法对其进行最小化从而求解得到模型对应的权重参数，即

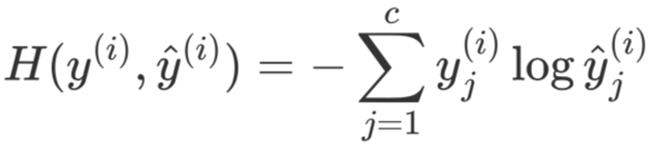
其中y(i)y^{(i)}和y ̂^{(i)}分别表示第i个样本的真实概率分布和预测概率分布，yj(i)y_j^{(i)}和y ̂_j^{(i)}分别表示第i个样本第jj个类别对应的概率值，cc表示分类类别数，loglog表示取自然对数。因此，对于包含有m个样本的训练集来说，其损失函数为

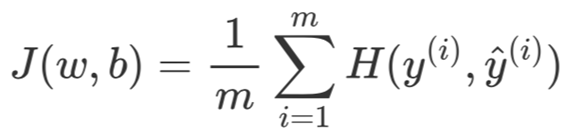
其中，ww和bb表示整个模型的所有参数，同时称其为交叉熵损失函数。

最后,这里有两点值得注意:

1.回归模型一般来讲是指对连续值进行预测的一类模型而分类模型则是指对离散值(类标)进行预测的一类模型,但逻辑回归和Softmax回归例外;

2.Softmax回归也是一个单层神经网络且直接对各个原始特征的线性组合进行归一化操作,但是Softmax这一操作却可以运用到每个神经网络的最后一层,而这也是深度学习中分类模型的标准操作。

5.Softmax回归的简洁实现

由于在深度学习中训练集的数量巨大很难一次同时计算所有权重参数在所有样本上的梯度，因此可以采用随机梯度下降（Stochastic Gradient Descent）或者是小批量梯度下降（Mini-batch Gradient Descent）来解决这个问题。相比于梯度下降算法在所有样本上计算得到目标函数关于参数的梯度然后再进行平均，随机梯度下降算法的做法是每次迭代时只取一个样本来计算权重参数对应的梯度。由于随机梯度下降是基于每个样本进行梯度计算，所以在迭代过程中每次计算得到的梯度值抖动很大，因此在实际情况中我们会每次选择一小批量的样本来计算权重参数的梯度，而这个批量的大小在深度学习中就被称为批大小（Batch Size）。

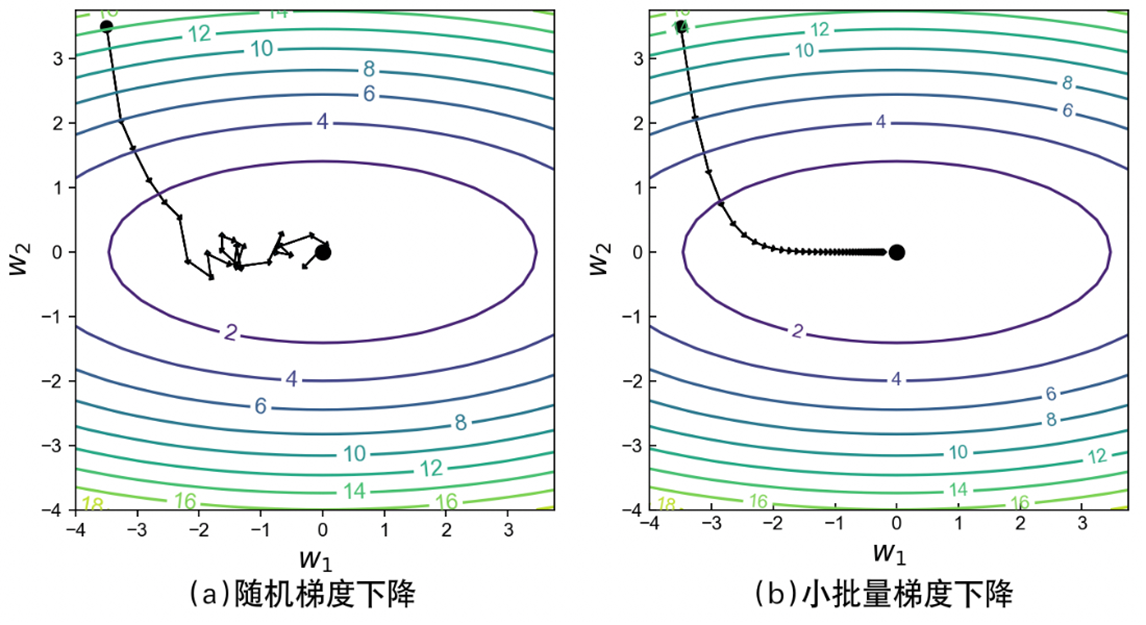
如图所示，环形曲线表示目标函数对应的等高线，左右两边分别为随机梯度下降算法和梯度下降算法求解参数w_1和w_2的模拟过程。从左侧的优化过程可以看出，尽管随机梯度下降算法最终也能近似求解得到最优解，但是在整个迭代优化过程中梯度却不稳定，极有可能导致陷入局部最优解当中。

5.1 DataLoader使用

在PyTorch中可以借助DataLoader模块来快速完成小批量数据的迭代生成。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

import torchvision
from torch.utils.data import DataLoader
from torchvision.datasets import MNIST
from torch.utils.data import TensorDataset
import torch
import numpy as np


def DataLoader1():
    data_loader = MNIST(root='~/Datasets/MNIST',
                               download=True,
                               transform=torchvision.transforms.ToTensor())
    data_iter = DataLoader(data_loader, batch_size=32)
    for (x, y) in data_iter:
        print(x.shape, y.shape)
        break


def DataLoader2():
    x = torch.tensor(np.random.random([100, 3, 16, 16]))
    y = torch.tensor(np.random.randint(0, 10, 100))
    dataset = TensorDataset(x, y)
    data_iter = DataLoader(dataset, batch_size=32)
    for (x, y) in data_iter:
        print(x.shape, y.shape)
        break


if __name__ == '__main__':
    DataLoader1()
    DataLoader2()

    
#输出结果
torch.Size([32, 1, 28, 28]) torch.Size([32])
torch.Size([32, 3, 16, 16]) torch.Size([32])

5.2 nn.CrossEntropyLoss()使用

在分类任务中会使用交叉熵来作为目标函数，且计算交叉熵损失之前需要对预测概率进行Softmax归一化。在PyTorch中可以借助nn.CrossEntropyLoss()模块来一次完成这两步计算过程。

1
2
3
4
5
6
7
8
if __name__ == '__main__':
    logits = torch.tensor([[0.5, 0.3, 0.6], [0.5, 0.4, 0.3]])#模拟模型输出结果，包含两个样本三个结果
    y = torch.LongTensor([2, 0])#两个样本的正确标签
    #注意：nn.CrossEntropyLoss()计算交叉熵损失时接受的正确标签是非One-Hot的编码形式。
    loss = nn.CrossEntropyLoss(reduction='mean')  # 返回的均值是除以的每一批样本的个数（不一定是batch_size）
    #mean表示返回样本损失的均值，sum表示样本损失和
    l = loss(logits, y)#计算交叉熵
    print(l)  # tensor(0.9874)

完整代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

import torch.nn as nn
import torch
import numpy as np


def crossEntropy(y_true, logits):
    loss = y_true * np.log(logits)  # [m,n]
    return -np.sum(loss) / len(y_true)


def softmax(x):
    s = np.exp(x)
    return s / np.sum(s, axis=1, keepdims=True)

#
if __name__ == '__main__':
    logits = torch.tensor([[0.5, 0.3, 0.6], [0.5, 0.4, 0.3]])
    y = torch.LongTensor([2, 0])
    loss = nn.CrossEntropyLoss(reduction='mean')  # 返回的均值是除以的每一批样本的个数（不一定是batch_size）
    l = loss(logits, y)
    print(l)  # tensor(0.9874)

    logits = np.array([[0.5, 0.3, 0.6], [0.5, 0.4, 0.3]])
    y = np.array([2, 0])
    y_one_hot = np.eye(3)[y]
    print(crossEntropy(y_one_hot, softmax(logits)))  
    
    # 0.9874308806774512

6.手写体分类实现

pytorch实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55

from torchvision.datasets import MNIST
import torchvision.transforms as transforms
from torch.utils.data import DataLoader
import torch.nn as nn
import torch
import matplotlib.pyplot as plt


def load_dataset():
    data = MNIST(root='~/Datasets/MNIST', train=True, download=True,
                 transform=transforms.ToTensor())
    return data


def visualization_loss(losses):
    plt.plot(range(len(losses)), losses)
    plt.xlabel('迭代次数', fontsize=15)
    plt.ylabel('损失值', fontsize=15)
    plt.rcParams['font.sans-serif'] = ['Arial Unicode MS']
    # plt.ylim(-.05, 0.5)
    plt.tight_layout()
    plt.show()


def train(data):
    epochs = 2
    lr = 0.03
    batch_size = 128
    input_node = 28 * 28
    output_node = 10
    losses = []
    data_iter = DataLoader(data, batch_size=batch_size, shuffle=True)
    net = nn.Sequential(nn.Flatten(), nn.Linear(input_node, output_node))
    loss = nn.CrossEntropyLoss()  # 定义损失函数
    optimizer = torch.optim.SGD(net.parameters(), lr=lr)  # 定义优化器
    for epoch in range(epochs):
        for i, (x, y) in enumerate(data_iter):
            logits = net(x)
            l = loss(logits, y)
            optimizer.zero_grad()
            l.backward()
            optimizer.step()  # 执行梯度下降
            acc = (logits.argmax(1) == y).float().mean().item()
            print(f"Epochs[{epoch + 1}/{epochs}]--batch[{i}/{len(data_iter)}]"
                  f"--Acc: {round(acc, 4)}--loss: {round(l.item(), 4)}")
            losses.append(l.item())
    return losses


if __name__ == '__main__':
    data = load_dataset()
    losses = train(data)
    visualization_loss(losses)

从0实现多层神经网络的手写体分类

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220

import numpy as np
from torchvision.datasets import MNIST
import torchvision.transforms as transforms


def load_dataset():
    """
    构造数据集
    :return: x: shape (60000, 784)
             y: shape (60000, )
    """
    data = MNIST(root='~/Datasets/MNIST', download=True,
                 transform=transforms.ToTensor())
    x, y = [], []
    for img in data:
        x.append(np.array(img[0]).reshape(1, -1))
        y.append(img[1])
    x = np.vstack(x)
    y = np.array(y)
    return x, y


def gen_batch(x, y, batch_size=64):
    """
    构建迭代器
    :param x: 
    :param y: 
    :param batch_size: 
    :return: 
    """
    s_index, e_index, batches = 0, 0 + batch_size, len(y) // batch_size
    if batches * batch_size < len(y):
        batches += 1
    for i in range(batches):
        if e_index > len(y):
            e_index = len(y)
        batch_x = x[s_index:e_index]
        batch_y = y[s_index: e_index]
        s_index, e_index = e_index, e_index + batch_size
        yield batch_x, batch_y


def sigmoid(z):
    return 1 / (1 + np.exp(-z))


def crossEntropy(y_true, logits):
    """
    计算交叉熵
    :param y_true:  one-hot [m,n]
    :param logits:  one-hot [m,n]
    :return:
    """
    loss = y_true * np.log(logits)
    return -np.sum(loss) / len(y_true)


def softmax(x):
    """
    :param x: [m,n]
    :return: [m,n]
    """
    s = np.exp(x)
    # 因为np.sum(s, axis=1)操作后变量的维度会减一，为了保证广播机制正常
    # 所以设置 keepdims=True 保持维度不变
    return s / np.sum(s, axis=1, keepdims=True)


def forward(x, w1, b1, w2, b2, w3, b3):
    """
    前向传播
    :param x: shape: [m,input_node]
    :param w1: shape: [input_node,hidden_node]
    :param b1: shape: [hidden_node]
    :param w2: shape: [hidden_node,output_node]
    :param b2: shape: [output_node]
    :return:
    """
    z2 = np.matmul(x, w1) + b1  # [m,n] @ [n,h] + [h] = [m,h]
    a2 = sigmoid(z2)  # a2:[m,h]
    z3 = np.matmul(a2, w2) + b2
    a3 = sigmoid(z3)
    z4 = np.matmul(a3, w3) + b3  # w2: [h,c]
    a4 = softmax(z4)
    return a4, a3, a2


def backward(a4, a3, a2, a1, w3, w2, y):
    m = a4.shape[0]
    delta4 = a4 - y  # [m,c]
    grad_w3 = 1 / m * np.matmul(a3.T, delta4)  # [hidden_nodes,c]
    grad_b3 = 1 / m * np.sum(delta4, axis=0)  # [c]

    delta3 = np.matmul(delta4, w3.T) * (a3 * (1 - a3))  # [m,hidden_nodes]
    grad_w2 = 1 / m * np.matmul(a2.T, delta3)  # [hidden_nodes,hidden_nodes]
    grad_b2 = 1 / m * (np.sum(delta3, axis=0))  # [hidden_nodes,]

    delta2 = np.matmul(delta3, w2.T) * (a2 * (1 - a2))  # [m,hidden_nodes]
    grad_w1 = 1 / m * np.matmul(a1.T, delta2)  # [input_nodes, hidden_nodes]
    grad_b1 = 1 / m * (np.sum(delta2, axis=0))  # [hidden_nodes,]
    return [grad_w1, grad_b1, grad_w2, grad_b2, grad_w3, grad_b3]


def gradient_descent(grads, params, lr):
    """
    梯度下降
    :param grads:
    :param params:
    :param lr:
    :return:
    """
    for i in range(len(grads)):
        params[i] -= lr * grads[i]
    return params


def accuracy(y_true, logits):
    """
    用于计算单个batch中预测结果的准确率
    :param y_true:
    :param logits:
    :return:
    """
    acc = (logits.argmax(1) == y_true).mean()
    return acc


def evaluate(x, y, net, w1, b1, w2, b2, w3, b3):
    """
    用于计算整个数据集所有预测结果的准确率
    :param x: [m,n]
    :param y: [m,]
    :param net:
    :param w1: [m,h]
    :param b1: [h,]
    :param w2: [h,c]
    :param b2: [c,]
    :return:
    """
    acc_sum, n = 0.0, 0
    for x, y in gen_batch(x, y):
        logits, _, _ = net(x, w1, b1, w2, b2, w3, b3)
        acc_sum += (logits.argmax(1) == y).sum()
        n += len(y)
    return acc_sum / n


def visualization_loss(losses):
    import matplotlib.pyplot as plt
    plt.plot(range(len(losses)), losses)
    plt.xlabel('迭代次数', fontsize=15)
    plt.ylabel('损失值', fontsize=15)
    plt.rcParams['font.sans-serif'] = ['Arial Unicode MS']
    # plt.ylim(-.05, 0.5)
    plt.tight_layout()
    plt.show()


def train(x_data, y_data):
    input_nodes = 28 * 28
    hidden_nodes = 1024
    output_nodes = 10
    epochs = 2
    lr = 0.03
    losses = []
    batch_size = 64
    w1 = np.random.uniform(-0.3, 0.3, [input_nodes, hidden_nodes])
    b1 = np.zeros(hidden_nodes)

    w2 = np.random.uniform(-0.3, 0.3, [hidden_nodes, hidden_nodes])
    b2 = np.zeros(hidden_nodes)

    w3 = np.random.uniform(-0.3, 0.3, [hidden_nodes, output_nodes])
    b3 = np.zeros(output_nodes)

    for epoch in range(epochs):
        for i, (x, y) in enumerate(gen_batch(x_data, y_data, batch_size)):
            logits, a3, a2 = forward(x, w1, b1, w2, b2, w3, b3)
            y_one_hot = np.eye(output_nodes)[y]
            loss = crossEntropy(y_one_hot, logits)
            grads = backward(logits, a3, a2, x, w3, w2, y_one_hot)
            w1, b1, w2, b2, w3, b3 = gradient_descent(grads,
                                                      [w1, b1, w2, b2, w3, b3], lr)
            if i % 5 == 0:
                acc = accuracy(y, logits)
                print(f"Epochs[{epoch + 1}/{epochs}]--batch[{i}/{len(x_data) // batch_size}]"
                      f"--Acc: {round(acc, 4)}--loss: {round(loss, 4)}")
            losses.append(loss)
    acc = evaluate(x_data, y_data, forward, w1, b1, w2, b2, w3, b3)
    print(f"Acc: {acc}")
    return losses, w1, b1, w2, b2, w3, b3


def prediction(x, w1, b1, w2, b2, w3, b3):
    x = x.reshape(-1, 784)
    logits, _, _ = forward(x, w1, b1, w2, b2, w3, b3)
    return np.argmax(logits, axis=1)


#
#
if __name__ == '__main__':
    x, y = load_dataset()
    losses, w1, b1, w2, b2, w3, b3 = train(x, y)
    visualization_loss(losses)
    y_pred = prediction(x[0], w1, b1, w2, b2, w3, b3)
    print(f"预测标签为: {y_pred}, 真实标签为: {y[0]}")

    # Epochs[1/2]--batch[0/937]--Acc: 0.1406--loss: 5.1525
    # Epochs[1/2]--batch[5/937]--Acc: 0.1562--loss: 2.5282
    # Epochs[1/2]--batch[10/937]--Acc: 0.2188--loss: 2.3137
    # Epochs[1/2]--batch[15/937]--Acc: 0.2812--loss: 2.0799
    # Epochs[1/2]--batch[20/937]--Acc: 0.5469--loss: 1.5729
    # Epochs[1/2]--batch[25/937]--Acc: 0.5--loss: 1.5751
    # ......
    # Epochs[2/2]--batch[930/937]--Acc: 0.9844--loss: 0.0769
    # Epochs[2/2]--batch[935/937]--Acc: 1.0--loss: 0.0262
    # Acc: 0.9115333333333333

参考

王成、黄晓辉——《跟我一起学深度学习》

李沐——《动手学深度学习》

深度学习
#大模型 #深度学习
逻辑回归到Softmax回归
https://this-is-kuo.github.io/2025/10/26/逻辑回归到Softmax回归/
作者
Kuo
发布于
2025年10月26日
许可协议