扩散模型

扩散模型（Diffusion Model）零基础·超详细学习笔记

从“完全不懂” → “能完整复述 + 自己推公式”

---

一、扩散模型到底在解决什么问题？

1.1 生成模型要干的事（最原始版本）

所有生成模型，本质都在做一件事：

学会“真实数据长什么样”，然后自己“造”一个出来

比如图像生成：

• 输入：随机噪声
• 输出：一张“看起来像真的”图片

文件中用一句话概括：

影像生成模型的目标是让「模型生成的数据分布 ≈ 真实数据分布」

---

1.2 以前的模型为什么难？

方法	问题
GAN	训练不稳定、容易崩
VAE	图像模糊
Autoregressive	太慢

👉 扩散模型的出发点非常“笨”，但极其稳定。

---

二、扩散模型的“笨办法”：先毁掉，再救回来

2.1 一个反直觉但关键的想法

扩散模型不是直接学“怎么生成图像”，而是：

先把一张真实图片，慢慢“毁掉”成纯噪声
再学“如何一步一步救回来”

课件里反复用这句话强调思想本质 。

---

2.2 正向过程（Forward Process）：加噪声

假设你有一张真实图片 $x_0$。

我们做下面这件事：

• 第 1 步：加一点点噪声 → $x_1$
• 第 2 步：再加一点 → $x_2$
• …
• 第 1000 步：几乎变成纯随机噪声 → $x_T$

⚠️ 这个过程是我们人为设计的，不需要学习

---

2.3 为什么要“慢慢”加噪声？

如果你一次性把图片变成噪声：

• 模型根本学不会
• 信息完全丢失

慢慢加噪声的好处：

• 每一步只“破坏一点点”
• 反过来“修一点点”是可学习的

---

三、正向扩散的数学，其实比你想象的简单

3.1 每一步加噪声在做什么？

课件定义：

$$x_t = \sqrt{1-\beta_t}x_{t-1} + \sqrt{\beta_t}\epsilon$$

别怕，我们逐项解释：

• $x_{t-1}$：上一步的图
• $\epsilon$：标准高斯噪声（随机）
• $\beta_t$：一个很小的数（比如 0.0001）

意思就是：

新图 = 原图 × 一点点 + 噪声 × 一点点

---

3.2 最重要的一步：可以“一步到位”

这是 扩散模型训练能跑起来的关键：

$$x_t = \sqrt{\bar{\alpha}_t}x_0 + \sqrt{1-\bar{\alpha}_t}\epsilon$$

含义翻译成人话：

不管你要第几步的噪声图，都可以直接从原图算出来

这意味着：

• 不用真的跑 1000 步
• 训练时随便抽一个 t 就行

课件中反复强调这一点 。

---

四、真正要学的部分：反向过程（去噪）

4.1 模型到底在学什么？

我们已经知道：

• 怎么从 $x_0$ → $x_t$（加噪）
• 那生成时要做什么？

👉 反过来：从 $x_t$ → $x_{t-1}$

这一步是未知的，需要神经网络学习。

---

4.1.1 Noise Predicter 模块在扩散模型中的地位

回顾一句核心话：

扩散模型 = 不断调用同一个 Noise Predicter 网络

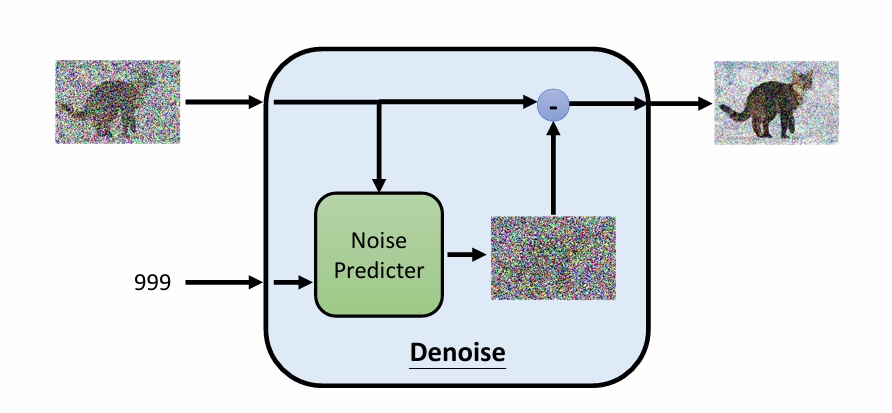
也就是说：

• 没有 1000 个网络
• 只有一个网络
• 在不同时间步 $t$ 上反复使用

📌 所以理解 Noise Predicter 模块 = 理解扩散模型本体

4.1.2 扩散模型中的 Noise Predictor（噪声预测器）

这是扩散模型唯一真正“学习”的模块

Noise Predictor 是一个神经网络，用来预测：在第 t 步中，被加到数据里的那一部分高斯噪声

严格来说，网络预测的是噪声 ε，“去噪”是通过公式计算得到的结果，而不是网络直接输出。

数学上：

$$\epsilon_\theta(x_t, t \;[, c])$$

这不是命名习惯问题，而是模型本质问题：

• ❌ 它不是“去噪器”
• ❌ 它不直接输出干净样本
• ✅ 它只做一件事：预测噪声

---

4.2 Noise Predictor 模块的输入 / 输出（极其重要）

4.2.1 输入是什么？

Noise Predictor 网络每一次调用，输入是：

1. 当前带噪数据

   图像扩散：$x_t \in \mathbb{R}^{H\times W\times C}$

   Stable Diffusion：latent $z_t \in \mathbb{R}^{h\times w\times c}$

2. 时间步 t

   一个整数(1~T)

   但不能直接喂给网络（后面解释）

3. （可选）条件信息

   比如 text embedding（Stable Diffusion）

---

4.2.2 输出是什么？

只输出一件东西：

👉 当前这一步中，被加进去的噪声 $\epsilon$

形状：

• 和输入图像/latent 一模一样
• 不是标量
• 是一个“噪声图”

⚠️ 非常重要的认知纠正：

• 网络 不是 输出“去噪后的图”
• 网络 不是 输出“干净图像”
• 网络 只负责猜噪声

---

4.3 时间步 t 是怎么喂给网络的？

4.3.1 为什么 t 不能直接当整数用？

如果你直接输入：

t = 532

问题：

• 神经网络无法理解“532 比 100 更接近 533”
• 离散整数 ≠ 连续信息

4.3.2 时间嵌入（Time Embedding）

扩散模型使用的几乎都是：

Sinusoidal Positional Embedding（和 Transformer 一样）

做法：

• 把 t 映射成一个高维向量
• 包含不同频率的 sin / cos
• 表示“噪声强度阶段”

直觉理解：

网络不是在看“第几步”，而是在看“噪声有多重”

4.4 Denoise 模块的网络结构：U-Net

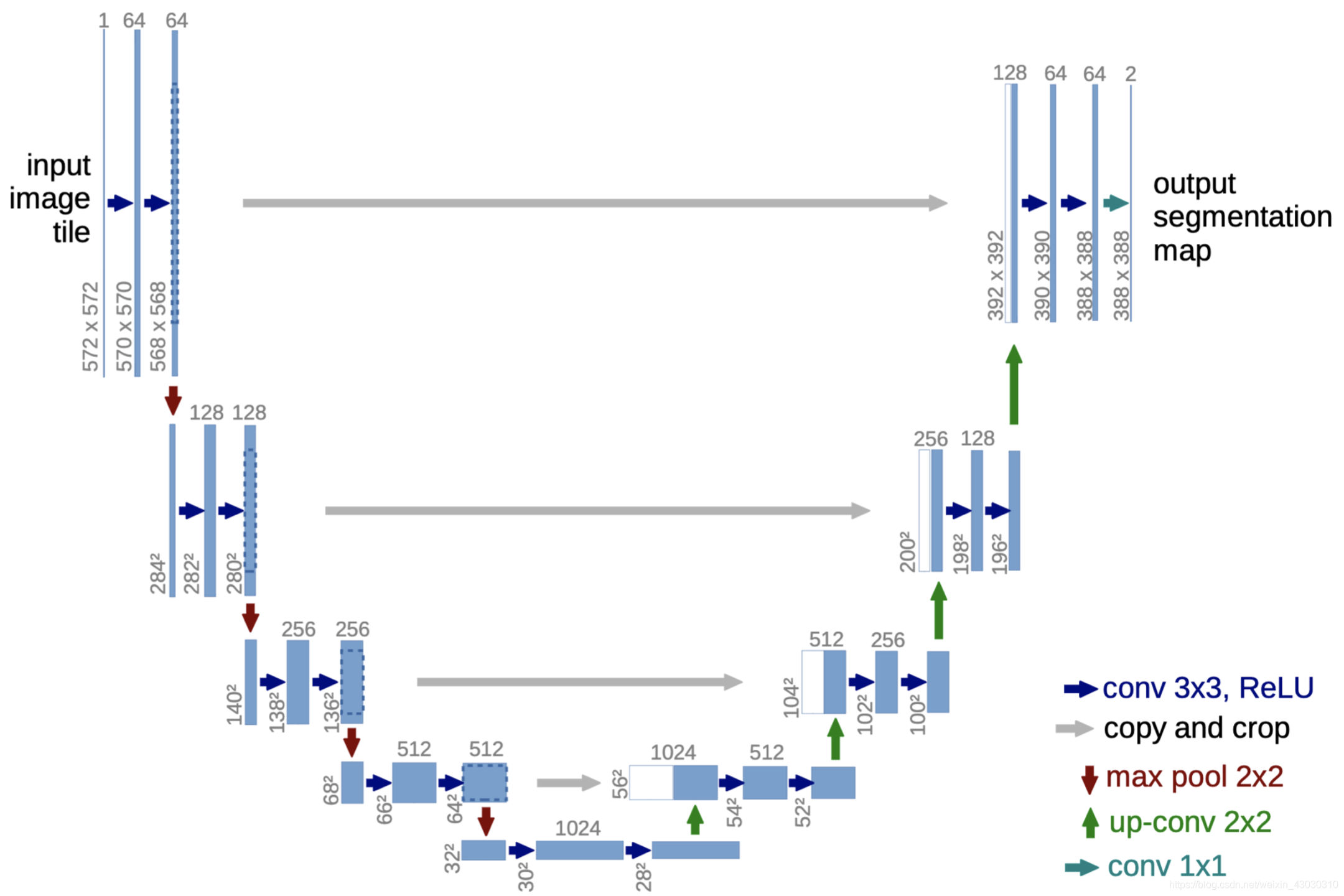
几乎所有扩散模型，都用 U-Net

• 收缩路径（ Encoder）： U 形的左半部分。
• 扩展路径（ Decoder）： U 形的右半部分。
• 跳跃连接（Skip Connections）： 连接左右两部分的“桥梁”。

---

4.4.1 为什么是 U-Net？

扩散任务的特点：

• 输入和输出 形状完全一样
• 需要同时：
  • 看整体结构（轮廓）
  • 看局部细节（纹理）

U-Net 天生满足：

• Encoder：看全局
• Decoder：恢复细节
• Skip Connection：保留空间信息

---

4.4.2 U-Net 的三大部分

（1）Encoder（下采样）

作用：

• 降分辨率
• 提高感受野
• 理解“这张图整体是什么”

结构：

• Conv → ResBlock → Downsample
• 每降一层，通道数 ↑

---

（2）Bottleneck（最底层）

作用：

• 信息融合中心
• 最抽象、最全局的表示

在 Stable Diffusion 中：

• Self-Attention / Cross-Attention 就在这里大量使用
• “Attention 主要出现在中低分辨率层，用于全局建模”

---

（3）Decoder（上采样）

作用：

• 把抽象特征还原成空间结构
• 恢复细节

关键点：

• 和 Encoder 对称
• 每一层都有 Skip Connection

---

4.4.3 Skip Connection 的真正意义

不是“为了防止梯度消失”这么简单。

在扩散中，Skip Connection 的意义是：

低层保留“哪里有东西”，高层决定“是什么东西”

这对去噪至关重要。

---

五、训练过程：一步一步“造假题”教模型

5.1 训练数据怎么来？

训练时，每一步都在做这件事：

1. 随机抽一张真实图片 $x_0$
2. 随机抽一个时间步 $t$
3. 随机生成一个噪声 $\epsilon$
4. 算出 $x_t$
5. 把 $(x_t, t)$ 喂给网络
6. 让网络猜 $\epsilon$

---

5.2 损失函数居然只是 MSE(均方误差）？

损失函数：

$$\mathcal{L} = |\epsilon - \epsilon_\theta(x_t, t)|^2$$

为什么这么简单？

• 这是从最大似然（MLE）严格推导出来的
• 等价于优化 ELBO
• 本质是 Score Matching

👉 看起来像回归，实际上是概率建模

---

六、生成（Inference）：模型是如何“画”图的？

6.1 生成流程

生成时，完全不需要真实图片：

1. 从纯噪声 $x_T \sim \mathcal{N}(0, I)$ 开始

2. for t = T → 1：

   • 用网络预测噪声
   • 把噪声“减掉一点”
   • 得到更干净的图

3. 最后得到 $x_0$

---

6.2 为什么每一步要“随机采样”？

• 如果只取 Gaussian 的均值

• 所有样本都会变得很像

• 多样性消失

  DDIM / deterministic sampler 可以去掉随机性

  但牺牲多样性换速度

这和语言模型：

• greedy decoding
• beam search 崩坏

是同一个问题 。

---

Diffusion Model（DDPM）推导讲义

---

0. 问题设定

我们的目标是学习一个生成模型，使其能够从随机噪声中采样出服从真实数据分布 $p_{\text{data}}(x)$ 的样本。

直接建模复杂高维分布 $p(x)$ 非常困难，因此扩散模型采用了一种 “先破坏、再修复” 的策略。

---

1. 正向扩散过程（Forward Process）

我们人为定义一个逐步加噪的马尔可夫链：

$$q(x_t \mid x_{t-1})=\mathcal{N}\big(\sqrt{1-\beta_t} x_{t-1},\beta_t I\big),\qquad t = 1,\dots,T$$

其中：

• $\beta_t \in (0,1)$ 为预先设定的噪声调度
• 每一步仅加入少量高斯噪声
• 正向过程 不需要学习

---

2. 一步到位采样公式（关键）

定义：

$$\alpha_t = 1 - \beta_t,\qquad\bar{\alpha}_t = \prod_{i=1}^t \alpha_i$$

🔹 $\alpha_t = 1-\beta_t$

👉 定义每一步“还保留多少原图信息”

• $\beta_t$：这一小步丢多少信息
• $\alpha_t$：这一小步保留多少信息

🔹$\bar{\alpha}_t = \prod_{i=1}^t \alpha_i$

👉 定义“到第 t 步为止，还剩多少原始信号”

这是一个累计量：

• 第 1 步保留 $\alpha_1$
• 第 2 步再乘 $\alpha_2$
• …
• 第 t 步乘完，剩下 $\bar{\alpha}_t$

📌 所以：
$\bar{\alpha}_t=$
从 $x_0$ 传到 $x_t$ 的“信号衰减系数”

可以证明，任意时刻 $x_t$ 都可以直接由原始样本 $x_0$ 采样得到：

$$\boxed{x_t=\sqrt{\bar{\alpha}_t}, x_0+\sqrt{1-\bar{\alpha}_t}\varepsilon,\quad\varepsilon \sim \mathcal{N}(0, I)}$$

重要意义：

• 训练时无需真的执行 $t$ 步扩散
• 可以随机采样任意时间步 $t$
• 这是扩散模型可训练的核心原因

---

3. 反向过程建模（Reverse Process）

正向过程已知，而反向过程 $x_t \rightarrow x_{t-1}$ 是未知的。

我们用参数化高斯分布近似真实反向分布：

$$p_\theta(x_{t-1} \mid x_t)=\mathcal{N}\big(\mu_\theta(x_t, t),\sigma_t^2 I\big)$$

学习的关键在于 如何建模均值 $\mu_\theta$。

---

4. 为什么预测噪声是最优选择（核心推导）

由第 2 节的一步到位公式，可以反解得到：

$$\boxed{x_0=\frac{1}{\sqrt{\bar{\alpha}_t}}\left(x_t-\sqrt{1-\bar{\alpha}_t} \varepsilon\right)}$$

这表明：

如果我们能够准确预测噪声 $\varepsilon$，就可以恢复出原始数据 $x_0$。

因此，我们令神经网络学习一个 噪声预测器：

$$\varepsilon_\theta(x_t, t) \approx \varepsilon$$

---

5. 反向均值的显式形式

将噪声预测器代入反向过程，可得反向均值的闭式表达：

$$\boxed{\mu_\theta(x_t, t)=\frac{1}{\sqrt{\alpha_t}}\left(x_t-\frac{\beta_t}{\sqrt{1-\bar{\alpha}_t}}\varepsilon_\theta(x_t, t)\right)}$$

关键理解：

• 神经网络仅预测噪声
• “去噪”并非网络直接输出，而是通过公式计算得到

---

6. 训练目标函数

扩散模型的训练目标源自最大似然估计（MLE），通过 ELBO 推导可化简为：

$$\boxed{\mathcal{L}_{\text{simple}}=\mathbb{E}_{x_0,\varepsilon,t}\left[||\varepsilon -\varepsilon_\theta(x_t, t)||^2\right]}$$

该损失函数形式为 MSE，但其本质是：

• 变分推断
• Score Matching
• 概率密度梯度学习

---

7. 生成（Inference / Sampling）

生成阶段不需要真实样本：

1. 初始化

   $$x_T \sim \mathcal{N}(0, I)$$

2. 逐步反向采样

   $$x_{t-1}=\mu_\theta(x_t, t)*\sigma_t z,\quad z \sim \mathcal{N}(0, I)$$

3. 得到最终样本 $x_0$

随机项保证了生成样本的多样性；若去除随机项，即得到 DDIM 等确定性采样方法。

---

8. 总结

扩散模型通过逐步修正噪声分布，实现了对复杂数据分布的建模：

扩散模型不是直接生成样本，
而是在反复逼近真实数据分布的 score。

---